395 KiB
The Bethe Ansatz
- Introduction
- Models and eigenstates: the Coordinate Bethe Ansatz
- The Lieb-Liniger gas
- The Heisenberg spin-\(1/2\) chain
- Further spin chains
- Further continuum models
- Fermions on a lattice
- Impurity models
- Gaudin magnets
- Ground states: identification, properties and excitations
- Equilibrium at finite \(T\): the Thermodynamic Bethe Ansatz
- The Algebraic Bethe Ansatz
- General considerations and the Yang-Baxter equation
- Constructing \(R\) matrices
- Constructing integrable models
- ABA for the isotropic \(S=1/2\) antiferromagnet (\(XXX\) model)
- Another example: the trigonometric \(R\)-matrix and the anisotropic \(S=1/2\) antiferromagnet (\(XXZ\) model)
- Scalar products: Slavnov's formula
- Matrix elements of physical operators
- Dynamical correlation functions
- Integrability out of equilibrium
- Literature
This site presents a collection of online resources on the Bethe Ansatz and related concepts used in the study of integrable models of quantum mechanics.
The aim is to provide a compendium of models, methods and results on these (in many ways) exceptional many-body systems, in order to make their fascinating physics accessible to a wider audience.
From the reader, a minimal undergraduate-level knowledge of quantum mechanics and of statistical mechanics is assumed. The material is presented in gradually increasing levels of difficulty: important concepts and methods are first introduced using the simplest available model, and therafter adapted or extended to others. Material of a more advanced or specialized nature is relegated to higher-level subsections.
You will find more details on the style and format in the Notes to the reader section.
This site is (and will remain) an open-ended construction project.
Introduction
What these pages are about
These online lecture notes concern models of many-body quantum mechanics which have the peculiarity of allowing for an exact solution of the Schrödinger problem, at least in principle. The toys are spins, bosons and fermions, the rules are the postulates of quantum mechanics, and the playground is either a chain (one-dimensional lattice) or a line.
Various sections cover the main general branches of the field:
- the Coordinate Bethe Ansatz (CBA) for solving the Schrödinger problem
- the Thermodynamic Bethe Ansatz (TBA) for computing equilibrium properties
- the Algebraic Bethe Ansatz (ABA) as a unifying, higher-level framework
- methods to extract quantitative results from otherwise intractable expressions for e.g. correlation functions
- some emerging ideas like the Quench Action, as a variational extension to treat out-of-equilibrium situations
The material is organized by (class of) model, with the bosonic Lieb-Liniger gas and the isotropic Heisenberg spin-\(1/2\) antiferromagnetic chain at the forefront, especially in the CBA and TBA parts. Later sections are arranged in a more ad hoc opportune fashion.
Why should you care?
Exactly solvable models have been around since shortly after the birth of quantum mechanics. The Bethe Ansatz appeared in 1931 in Bethe's paper 1931.Bethe.ZP.71 describing the eigenstates of Heisenberg's model of ferromagnetism. Ironically, Bloch had earlier (in 1930.Bloch.ZP.61) proposed a correct form for the Heisenberg model wavefunctions. He however succumbed to some (lazy) oversimplifications and failed to provide a correct basis of eigenstates; the Bloch Ansatz was thus stillborn. Undeterred by logarithms and arctangents, Bethe carefully constructed and counted the eigenstates, showing that their number coincided with the dimensionality of Hilbert space. The devil, but also eternal recognition, was indeed hidden in the details, and Bethe here arguably got his first lasting result as a midwife.
Bethe's solution however quickly obtained a reputation for being too complicated: already in 1938, Fritz Sauter complained in 1938.Sauter.AP.425 that
Die Lösung dieser Hauptaufgabe auf Grund der Wellenmechanik führt nach Bloch und Bethe bereits im einfachsten Fall einer linearen Kette zu so verwickelten Resultaten, dass für die Weiterrechnung damit relativ wenig gewonnen ist.
This approximately translates to:
The solution of this core problem of wave mechanics leads following Bloch and Bethe already in the simplest case of the linear chain to such intricate results, that little is gained as far as further calculations are concerned.
This sentiment persists to this day. When I was a young postdoc, a senior researcher confronted me in the corridor of the institute, displeased that I was focusing on (and perhaps too often expressing my predilection for) so-called "integrable models" of many-body physics. To him, I was simply wasting my time: these models were clearly exceptional (pathological even), fine-tuned, and most importantly totally divorced from physical reality. Studying them was a misdirected waste of effort, like medieval scholars asking how many angels can dance on the head of a pin.
There is no doubt that the study of the Bethe Ansatz requires handling complications which are rarely encountered in other simpler/simplified models. Sauter's assessment (and by extension the closed mind of my senior colleague) has however arguably been proven to be spectacularly wrong in the decades since it was made.
Today integrable models are used by a wider variety of researchers than ever. Their richness provides lasting delight to mathematicians. They provide much-needed confidence to theoretical physicists when exploring nonperturbative effects. They have also journeyed into the laboratories of condensed matter and atomic physics experimentalists, where some of their most spectacular features have been directly observed. Numerical methods have been battle-hardened by stringent tests from integrable models; the future development of out-of-equilibrium physics and of quantum information processing protocols and devices is certainly going to rely on exact solutions for orientation and certification.
Who knows what will come next; but as long as quantum mechanics stands (and there is no current indication that we are anywhere near abandoning that), integrable models will remain trustworthy lighthouses guiding the explorers of the stormy seas of many-body physics. This site is thus devoted to helping people see the treasures hidden in pinheads, and to befriend the many angel civilizations which are thriving in these seemingly boundless universes.
Notes to the reader
Section and equation labelling
For labelling sections and equations, I've preferred to use a semantic format instead of traditional numbers.
This has a number of advantages: the labelling is
- meaningful (at least occasionally)
- easier to remember in the long run
- stable under tree structure modifications
but also come with some things which need getting used to:
- the loss of clear notion of ordering
- abbreviations being as short as possible, thus sometimes obfuscating their original meaning
Section labelling: floated right next to the title of any section, you will see the label together with a permalink (pointing to the main site's version of that particular section). Under a section's headline, you will also sometimes see references (in small gray letters) to corresponding sections in complementary literature.
Parts identification: each part of the notes has a single-letter identifier, given in the following table:
| Part | Identifier |
| Introduction | i |
| Exact eigenstates: the Coordinate Bethe Ansatz | c |
| Ground states | g |
| Equilibrium thermodynamics | e |
| The Algebraic Bethe Ansatz | a |
| Dynamical correlation functions | d |
| Out of equilibrium | o |
| Literature | l |
Model identification: each model which is treated is given a one- or two-letter identifier according to the following table:
| Class | Model | Identifier | |
| Fundamental | f | ||
| Lieb-Liniger | l | ||
| Heisenberg spin-1/2 isotropic antiferromagnet | h | ||
| Further spin chains | sc | ||
| Ising | i | ||
| Heisenberg spin-1/2 isotropic ferromagnet | f | ||
| Heisenberg spin-1/2 planar model (XXZ with -1 < Δ < 1) | p | ||
| Heisenberg spin-1/2 axial antiferromagnet (XXZ with Δ > 1) | a | ||
| Heisenberg spin-1/2 axial ferromagnet (XXZ with Δ < -1) | af | ||
| Haldane-Shastry | hs | ||
| Inozemtsev | in | ||
| Babujian-Takhtajan | bt | ||
| Integrable spin-S | s | ||
| Further continuum | cm | ||
| Attractive Lieb-Liniger | al | ||
| Two-component Bose gas | b2 | ||
| Yang permutation | y | ||
| Fermions on a lattice | fl | ||
| t-J | tj | ||
| Hubbard | hu | ||
| Impurity models | im | ||
| Kondo or s-d | k | ||
| Anderson impurity | ai | ||
| Gaudin magnets | gm | ||
| Richardson | r | ||
| Gaudin magnets | g |
Equation labelling: similarly to sections, some (but not all) equations also carry a semantic label, given in parentheses to the right of the equation. As per sections, a permalink is also given, together with corresponding equation numbers in complementary literature.
Format
These lecture notes are published as HTML static files with source code written in Emacs Org mode.
All sources are preserved in a git repository at https://jscaux.org/git/jscaux/Bethe_Ansatz whose contents are publicly accessible.
Starting from the org source file, custom python and shell scripts are used to produce the final HTML output. These scripts can be found in the main repository's scripts folder.
Issues can be raised at https://jscaux.org/git/jscaux/Bethe_Ansatz/issues. Suggestions for improvements and extensions are welcome.
Copyright and license
All content here is published under the Creative Commons Attribution 4.0 International CC BY 4.0 license.
You are free to:
- Share — copy and redistribute the material in any medium or format
- Adapt — remix, transform, and build upon the material for any purpose, even commercially
Under the following terms:
- Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.
To cite material in these notes, please use the following format:
- J.-S. Caux, The Bethe Ansatz, https://integrability.org/, [section|equation] [identifier] ([permalink]).
For example:
- J.-S. Caux, The Bethe Ansatz, https://integrability.org/, section i.n.l (https://integrability.org/i_n_l.html)
- J.-S. Caux, The Bethe Ansatz, https://integrability.org/, equation l.H (https://integrability.org/c_l_l.html#l.H)
Contextual colors
Throughout these lecture notes, collapsible/expandable boxes with contextual colors are used, serving specific purposes:
Specific prerequisites for understanding the upcoming material
- you should already know this
- and this
- and that
Objectives for this part: what you should learn by reading this
- this
- and this
- and that
Core material: all equations are useful, but some are more useful than others.
Derivation of a particular (set of) equation(s).
Example of the concepts just covered.
Additional (contextual) information.
Additional historical context.
Acknowledgements
- Hans A. Bethe, for the hour in his office in early 1994, and his lasting tip You haff to vork fery feeery haaaaart!
-
- Vinet, for helping me substitute undergraduate condensed matter courses (the horror!) for a postgraduate "special topics" course (given by R. Weston) on quantum groups and the vertex operator approach, and for having ordered me to just sit on your … and write everything down, one day you'll understand
-
- Tsvelik, who as my doctoral supervisor really lived up to somebody who could really do this when it came to integrable models; the semi-private course he gave on this in the autumn of 1994 in his office in Brasenose College has for me been career-defining
-
- Saleur, who from Les Houches 1998 onwards has been my go-to father figure (at least for integrable field theory)
-
-
- Maillet, who by forcing me to spend at least minimal time in Lyon (when diapers pinned me home) initiated a very focused and determined period in my research work, and an even longer-lasting friendship
-
-
- Gaudin, whose book (in French!) helped my doctoral mind crystallize in the right way, and who later showed me such kindness and consideration when I tried to bring his work to a wider audience by translating it into English
-
- McCoy for the numerous hours of inspiring discussions on the science but also the past (and future!) history of the field
-
- Faddeev, whose self-invitation for a stay in Amsterdam after attending a talk of mine resulted in some memorable exchanges with countless insights and historical anectodes (and a wonderful portrait I still need to print properly).
[to be completed]
Zoology of models solvable by the Bethe Ansatz
Spin chains
Heisenberg chain
\[ H_{XXX} = J \sum_{j=1}^N {\bf S}_j \cdot {\bf S}_{j+1} \]
Anisotropic Heisenberg chain
\[ H_{XXZ} = J \sum_{j=1}^N \left[ S^x_j S^x_{j+1} + S^y_j S^y_{j+1} + \Delta (S^z_j S^z_{j+1} - 1/4) \right] \]
Fermions on a lattice
Hubbard
\[ H_{Hub} = -t \sum_{j,\sigma} (c^{\dagger}_{j\sigma} c_{j+1 \sigma} + \mbox{h.c.}) + U \sum_j n_{\uparrow} n_{\downarrow} \]
Impurity models
The Kondo (s-d exchange) model
\[ H_{K} = \int dx \sum_{a} c^{\dagger}_{a} (x) (-i \partial_x) c_a (x) + J \sum_{a,b} c^{\dagger}_a (0) {\boldsymbol \sigma}_{ab} c_b (0) \cdot {\boldsymbol S}_{\mbox{imp}} (0) \]
The Anderson model
\[ H_{And} = \int dx \sum_{a} c^{\dagger}_{a} (x) (-i \partial_x) c_a (x) + V (c^{\dagger}_a (0) d_a + d^{\dagger}_a c_a (0)) + \sum_a \varepsilon_d n_{d,a} + U n_{d,\uparrow} n_{d, \downarrow} \]
Continuum models
Lieb-Liniger
\[ H_{LL} = \int_0^L dx \left\{ \partial_x \Psi^{\dagger}(x) \partial_x \Psi(x) + c \Psi^{\dagger}(x) \Psi^{\dagger}(x) \Psi(x) \Psi(x) \right \} \]
and the generalization to an arbitrary symmetry of the wavefunction.
Gaudin-Yang
This is a model for spin-\(1/2\) fermions with an ultralocal contact interaction. The (first-quantized) Hamiltonian is precisely the same as the one of Lieb-Liniger. It was solved in 1967.Gaudin.PLA.24 and further in 1967.Yang.PRL.19.
Two-component Bose gas
This model is just like Lieb-Liniger, but for two colors of bosons: \[ H = \int_0^L dx \left\{ \sum_{a=1,2} \partial_x \Psi^{\dagger}_a(x) \partial_x \Psi_a(x) + c \sum_{a,b} \Psi^{\dagger}_a(x) \Psi^{\dagger}_b(x) \Psi_b(x) \Psi_a(x) \right \} \]
Yang permutation
This model is the further generalization of the Gaudin-Yang model to an arbitrary permutation group. The solution was provided by C.N. Yang in 1967.Yang.PRL.19. All previously-mentioned models with \(\delta\)-interaction can be viewed as special cases of this more general model.
Gaudin magnets and their generalizations
The Richardson model
\[ H_{Rich} = \sum_{\alpha,\sigma} \frac{\varepsilon_{\alpha}}{2} c^{\dagger}_{\alpha,\sigma} c_{\alpha,\sigma} - g \sum_{\alpha,\beta} c^{\dagger}_{\alpha,\uparrow}c^{\dagger}_{\alpha,\downarrow} c_{\beta,\downarrow} c_{\beta,\uparrow} \] also called the reduced-BCS model. The single-particle energies \(\varepsilon_{\alpha}\) are {\it arbitrary} parameters.
Gaudin magnets
\[ H_{G} = \sum_{\alpha} \varepsilon S^z_{\alpha} - g \sum_{\alpha,\beta} S^+_{\alpha} S^-_{\beta}. \]
Chronology of exactly solvable models
- 1928: Heisenberg publishes his model 1928.Heisenberg.ZP.49.
- 1930: Felix Bloch proposes an Ansatz for the wavefunctions 1930.Bloch.ZP.61: combinations of free waves. He simplifies the relative amplitudes too much. Finds too many solutions. Had it been done correctly, we'd today talk about the Bloch Ansatz.
- 1931: Hans Bethe obtains the correct form of the wavefunctions 1931.Bethe.ZP.71. Spends lots of effort showing that the counting of solutions gives the correct number of eigenstates. End: proposes to extend method to higher dimensions (in title of this paper: a very revealing \(1\)!)
- 1938: Hulthén obtains the ground-state energy of the Heisenberg model 1938.Hulthen.AMAF.26A.
- 1958: Orbach generalizes the solution to the Heisenberg model with anisotropic interactions (\(XXZ\) case) 1958.Orbach.PR.112.
- 1962: des Cloizeaux and Pearson obtain the correct spectrum of the Heisenberg antiferromagnet (spinon dispersion relation) 1962.desCloizeaux.PR.128, showing that it differs from Anderson's spin-wave theory predictions 1952.Anderson.PR.86 (the constant prefactor is different).
- 1963: Lieb and Liniger provide the exact solution of the 1d \(\delta\)-function interacting Bose gas 1963.Lieb.PR.130.1. Lieb studies the specturm and defines two basic types of excitations 1963.Lieb.PR.130.2.
- 1964: Griffiths obtains the magnetization curve of the Heisenberg model at \(T = 0\) 1964.Griffiths.PR.133.
- 1966: Yang and Yang prove Bethe's hypothesis for the ground-state of the Heisenberg chain 1966.Yang.PR.150.1. They study properties and applications in 1966.Yang.PR.150.2 and 1966.Yang.PR.151.
- 1967: Yang generalizes Lieb and Liniger's solution of the \(\delta\)-function interacting Bose gas to arbitrary permutation symmetry of the wavefunction 1967.Yang.PRL.19.
- 1968: Lieb and Wu solve the 1d Hubbard model 1968.Lieb.PRL.20.
- 1969: Yang and Yang obtain the thermodynamics of the Lieb-Liniger model 1969.Yang.JMP.10, providing the basis of the Thermodynamics Bethe Ansatz (TBA).
- 1971 (9 April): Gaudin obtains coupled nonlinear equations for the thermodynamics of the (anisotropic) Heisenberg chain (\(\Delta \geq 1\)) 1971.Gaudin.PRL.26.
- 1971 (9 April): Lai obtains the thermodynamics of interacting fermions in 1d 1971.Lai.PRL.26.
- 1971: Takahashi proposes equations for the thermodynamics of the Heisenberg model 1971.Takahashi.PTP.46.
- 1971 (13 September): Takahashi proposes equations for the thermodynamics of the gapless Heisenberg antiferromagnet (\(|\Delta| < 1\)) 1971.Takahashi.PLA.36.
- 1972 (May): Baxter solves the \(XYZ\) (8-vertex) model 1972.Baxter.AP.70.1, 1972.Baxter.AP.70.2.
- 1972 (December 1971): Johnson, McCoy and Lai criticise Takahashi's solution for \(|\Delta| < 1\) on the basis of the high-temperature expansion 1972.Johnson.PLA.38.
- 1972 (March/October): Johnson and McCoy use Gaudin's equations to obtain the low-\(T\) expansion of the free energy for \(|\Delta| \geq 1\) 1972.Johnson.PRA.6.
- 1972 (July/August): Takahashi and Suzuki obtain a corrected form of the coupled nonlinear integral equations for the thermodynamics of the Heisenberg chain for \(|\Delta| < 1\) 1972.Takahashi.PLA.41, 1972.Takahashi.PTP.48.
- 1972: Gaudin's internal Saclay report contains a conjecture for the norm of Bethe states.
- 1978-…: Faddeev, Sklyanin, Kulish, Takhtajan, etc. start developing the Algebraic Bethe Ansatz (see b-KBI and references therein).
- 1981: Faddeev and Takhtajan properly understand spinons as spin-\(1/2\) excitations 1981.Faddeev.PLA.85.
- 1981: Gaudin, McCoy and Wu obtain a conjecture for the norm of Bethe eigenstates of the Heisenberg chain 1981.Gaudin.PRD.23.
- 1982: Korepin proves Gaudin's conjecture for the norm of Bethe states using the ABA 1982.Korepin.CMP.86.
- 1988: Sklyanin extends the ABA to boundary cases 1988.Sklyanin.JPA.21.
- 1988-1989: Slavnov obtains expressions for scalar products (giving the density operator matrix element for the 1DBG) 1989.Slavnov.TMP.79 1990.Slavnov.TMP.82
- 1999: Solution of the quantum inverse problem. Calculation of matrix elements of the \(XXZ\) chain 1999.Kitanine.NPB.554.
Models and eigenstates: the Coordinate Bethe Ansatz
The Lieb-Liniger gas
The one-dimensional \(delta\)-interacting Bose gas, also known as the Lieb-Liniger model, is perhaps the least complicated quantum mechanical model of interacting particles allowing for a complete, formally exact solution of the Schrödinger problem using the Bethe Ansatz. Here, this exact solution is described.
Interacting particles in one dimension
Let us consider \(C\) different "colors" of particles living on a continuum interval in one dimension, with kinetic enegy given by free dynamics, each type of particle having mass \(m_c\), \(c = 1, ... ,C\). Let there be \(N_c\) particles of color \(c\), so that the total number of particles is \(N = \sum_c N_c\). Let the particles also interact with each other according to a color-dependent potential \(V^{c_1 c_2} (x)\) corresponding to a density-density interaction. A generic first-quantized Hamiltonian can be written
\begin{equation*} H = \sum_{c=1}^{C} \sum_{j_c = 1}^{N_c} \frac{-\hbar^2}{2m_c} \frac{\partial^2}{\partial_{x_{c,j_c}}^2} + \frac{1}{2} \sum_{c_1 \leq c_2 = 1}^{C} \sum_{j_1 = 1}^{N_{c_1}} \sum_{j_2 = 1}^{N_{c_2}} V^{c_1 c_2} (x_{c_1 j_1} - x_{c_2 j_2}). \end{equation*}Introducing a set of canonical field operators \(\psi_c (x,t)\) obeying the standard equal-time commutation relations
\begin{equation*} \left[ \psi_{c_1} (x_1), \psi^{\dagger}_{c_2} (x_2) \right]_\zeta = \delta_{c_1 c_2} \delta (x_1 - x_2), \hspace{1cm} \left[ \psi_{c_1} (x_1), \psi_{c_2} (x_2) \right]_\zeta = 0 = \left[ \psi^{\dagger}_{c_1} (x_2), \psi^{\dagger}_{c_2} (x_2) \right]_\zeta \end{equation*}in which \(\zeta = +\) for bosons and \(\zeta = -\) for fermions and \([,]_{\pm}\) denote the commutator (bosons) or anticommutator (fermions), the Hamiltonian is written in operator form (neglecting boundary terms) as
\begin{align*} H =& \sum_{c=1}^{C}\int dx ~\psi^\dagger_c (x) \left(-\frac{\hbar^2}{2m_c} \partial_x^2 \right) \psi_c(x) + \nonumber \\ &+ \frac{1}{2} \sum_{c_1 \leq c_2 =1}^{C}\int dx_1 dx_2~ V^{c_1 c_2} (x_1 - x_2) \psi^\dagger_{c_1} (x_1) \psi^\dagger_{c_2}(x_2) \psi_{c_2} (x_2) \psi_{c_1} (x_1). \end{align*}Interactions affect bosonic and fermionic systems in dramatically different ways. Spinless fermions develop a ground state Fermi segment (i.e. one-d sphere) of width \(2k_F\) (where \(k_F = \pi n\), \(n\) being their average density) with total energy density \(e_0 = \frac{k_F^3}{3\pi} = \frac{\pi^2}{3} n^3\), even if they do not interact with each other. A single species of fermions will moreover be completely insensitive to ultralocal (\(V(x_1 - x_2) \propto \delta (x_1 - x_2)\)) interactions due to the (real space) Pauli principle. On the other hand, the ground state of noninteracting bosons is a Bose-Einstein condensate-like state where all bosons simultaneously occupy the lowest-energy single-particle state allowed by the quantization conditions. Adding any form of interaction will dramatically alter this picture. Repulsive interactions will lead to the formation of an effective ground state Fermi segment; attractive interactions will cause a collapse to a new ground state where all particles are bound to each other.
The Lieb-Liniger model
Let us now specialize to the case of a single species of bosonic particles. We will thus use field operators \(\psi^\dagger (x)\), \(\psi(x)\) corresponding respectively to the creation/annihilation of a single particle at position \(x\), and obeying the canonical equal-time commutation relations
<<l.cr>>
The Hamiltonian we will consider takes the interaction potential \(V(x)\) to be zero-range (ultralocal), \(V(x) \equiv 2c \delta(x)\). For convenience, units are chosen such that \(\hbar = 1\) and \(2m = 1\). Taking the particle number to be fixed and equal to \(N\), this yields the (first-quantized version of the) Lieb-Liniger Hamiltonian
<<l.h1>>
whose second-quantized version is (written as the integral of a local, Hermitian Hamiltonian density)
<<l.h2>>
The equation of motion for the field operators is
<<nls>>
and is known as the nonlinear Schrödinger equation. The particle number and total momentum operators
<<l.np>>
give us the two simplest conservation laws →do{Write these laws as integrals of local densities; show they are locally conserved?}
\begin{equation*} \left[ \hat{H}_{\small LL}, \hat{N} \right] = 0, \hspace{10mm} \left[ \hat{H}_{\small LL}, \hat{P} \right] = 0. \end{equation*}Defining the Fock vacuum \(|0\rangle\) and its dual \(\langle 0 |\) as
<<l.fv>>
we can parametrize states in the Fock space having a fixed particle number \(N\) in terms of a complex-valued, space-dependent amplitude \(\Psi_N (x_1, ..., x_N)\),
<<l.psi>>
The time-independent Schrödinger equation for this quantum field theory,
<<l.se>>
is then equivalent to the quantum mechanical problem
<<l.se1>>
First term:
\begin{align*} \int_0^L dx \int_0^L dx_1 ... dx_N \Psi_N (x_1, ..., x_N) \partial_x \Psi^{\dagger}(x) \partial_x \left\{ \sum_{j=1}^N \delta(x - x_j) \prod_{l \neq j} \Psi^{\dagger}(x_l) \right\}|0\rangle \nonumber \\ = \int_0^L dx \int_0^L dx_1 ... dx_N \Psi_N (x_1, ..., x_N) \left\{ -\partial_x^2 \Psi^{\dagger}(x) \sum_{j=1}^N \delta(x - x_j) \prod_{l \neq j} \Psi^{\dagger}(x_l) \right\}|0\rangle \nonumber \\ = \int_0^L dx \int_0^L dx_1 ... dx_N \Psi_N (x_1, ..., x_N) \left\{ -\sum_{j=1}^N \delta(x - x_j) \partial_{x_j}^2 \right\} \prod_{l=1}^N \Psi^{\dagger}(x_l) |0\rangle \nonumber \\ = \int_0^L dx_1 ... dx_N \left\{ -\sum_{j=1}^N \partial_{x_j}^2 \Psi_N (x_1, ..., x_N) \right\} \prod_{l=1}^N \Psi^{\dagger}(x_l) |0\rangle \nonumber \\ \end{align*}Second term:
\begin{align*} \int_0^L dx \int_0^L dx_1 ... dx_N \Psi_N (x_1, ..., x_N) c \Psi^{\dagger}(x) \Psi^{\dagger}(x) \Psi(x) \Psi(x) \prod_{l=1}^N \Psi^{\dagger}(x_l) |0\rangle \nonumber \\ = \int_0^L dx \int_0^L dx_1 ... dx_N \Psi_N (x_1, ..., x_N) ~c \Psi^{\dagger}(x) \Psi^{\dagger}(x) \sum_{j,k; j\neq k} \delta (x - x_j) \delta (x - x_k) \prod_{l \neq j,k} \Psi^{\dagger} (x_l) |0\rangle \nonumber \\ = \int_0^L dx \int_0^L dx_1 ... dx_N \Psi_N (x_1, ..., x_N) ~c \times \sum_{j,k; j\neq k} \Psi^{\dagger}(x_j) \Psi^{\dagger}(x_k) \delta (x - x_j) \delta (x_j - x_k) \prod_{l \neq j,k} \Psi^{\dagger} (x_l) |0\rangle \nonumber \\ = \int_0^L dx_1 ... dx_N \left\{c \sum_{j,k; j\neq k} \delta (x_j - x_k) \Psi_N (x_1, ..., x_N) \right\} \prod_{l=1}^N \Psi^{\dagger}(x_l) |0\rangle \nonumber \\ = \int_0^L dx_1 ... dx_N \left\{2c \sum_{j < k} \delta (x_j - x_k) \Psi_N (x_1, ..., x_N) \right\} \prod_{l=1}^N \Psi^{\dagger}(x_l) |0\rangle \end{align*}The interaction term prevents a straightforward solution of the Schrödinger equation for the Lieb-Liniger model using the standard tools of many-body theory. To gain some insights into the difficulties, let us proceed as follows. Taking the particles to be confined to an interval of length \(L\), Fourier transforms of the fields are defined as
<<l.f>>
giving canonical equal-time commutators
<<l.crf>>
For definiteness, we here impose periodic boundary conditions on the wavefunctions, meaning that the momenta are given by
\begin{equation*} k \in \{ k_n \}, \hspace{10mm} k_n = \frac{2\pi}{L} n, \hspace{10mm} n \in \mathbb{Z}. \end{equation*}The Lieb-Liniger Hamiltonian is then
<<l.hf>>
The interaction term thus induces transitions between momentum occupation modes which are of equal amplitude irrespective of the momentum transfer. Trying to apply perturbation theory in the interaction around \(c=0\), we face many difficulties associated to the fact that we are perturbing around a macroscopically degenerate state (all bosons in the \(k=0\) mode). The next subsection provides an improved (though still inexact) line of attack.
Bogoliubov theory
It is possible to effectively resum terms in perturbation theory by following Bogoliubov's logic for quasi-degenerate gases. This begins by assuming that the lowest momentum mode is macroscopically occupied, namely that
\begin{equation*} \hat N = \hat N_0 + \frac{1}{L} \sum_{k \neq 0} \psi^\dagger_{k} \psi_{k}, \hspace{10mm} \frac{1}{L} \langle \psi^\dagger_{k=0} \psi_{k=0} \rangle \equiv N_0 = O(N). \end{equation*}Keeping only leading terms and performing a Bogoliubov transformation then gives the simplified Hamiltonian
<<l.hb>>
where \(\varepsilon^{\small Bog}\) is the well-known Bogoliubov dispersion relation
<<l.eb>>
and where the ground state energy is
<<l.e0b>>
in terms of the effective interaction parameter \(\gamma = c/n\).
Following Bogoliubov's logic, we assume that the lowest momentum mode is macroscopically occupied, namely that
\begin{equation*} \hat N = \hat N_0 + \frac{1}{L} \sum_{k \neq 0} \psi^\dagger_{k} \psi_{k}, \hspace{10mm} \frac{1}{L} \langle \psi^\dagger_{k=0} \psi_{k=0} \rangle \equiv N_0 = O(N). \end{equation*}In the Lieb-Liniger Hamiltonian represented in Fourier space l.hf, keeping only the leading terms involving at least two entries of the zero-momentum fields gives
\begin{equation*} H_{LL} \simeq \frac{c}{L^3} \Psi_0^\dagger \Psi_0^\dagger \Psi_0 \Psi_0 + \frac{1}{L} \sum_k k^2 \Psi^\dagger_k \Psi_k + \frac{2c}{L^3} \sum_{k > 0} \left[4 \Psi_0^\dagger \Psi_k^\dagger \Psi_0 \Psi_k + (\Psi_0^\dagger)^2 \Psi_k \Psi_{-k} + \Psi^\dagger_k \Psi^\dagger_{-k} \Psi_0^2 \right]. \end{equation*}Simple algebra then gives
\begin{equation*} H_{LL}^{\small Bog} = \frac{c N^2}{L} - \sum_{k>0} \left( k^2 + 2cn \right) + \frac{1}{L} \sum_{k>0} \left( k^2 + 2cn \right) \left( \begin{array}{cc} \psi^\dagger_k & \psi_{-k} \end{array} \right) \left( \begin{array}{cc} 1 & \gamma_k \\ \gamma_k & 1 \end{array} \right) \left( \begin{array}{c} \psi_k \\ \psi^\dagger_{-k} \end{array} \right) \end{equation*}where \(n = \frac{N}{L}\) and
\begin{equation*} \gamma_k \equiv \frac{2cn}{k^2 + 2cn}. \end{equation*}This can be diagonalized by a Bogoliubov transformation
\begin{equation*} \left( \begin{array}{c} \psi_k \\ \psi^\dagger_{-k} \end{array} \right) = \left( \begin{array}{cc} \cosh \theta_k & \sinh \theta_k \\ \sinh \theta_k & \cosh \theta_k \end{array} \right) \left( \begin{array}{c} \tilde{\psi}_k \\ \tilde{\psi}^\dagger_{-k} \end{array} \right), \hspace{10mm} \gamma_k = \tanh 2\theta_k. \end{equation*}The diagonalized quadratic form in the Hamiltonian then becomes \(\frac{1}{\cosh 2\theta_k} {\bf 1} = \left[ 1 - \gamma_k^2\right]^{1/2}\). The excitation energy \((k^2 + 2cn) (1-\gamma_k^2)\) then gives the well-known Bogoliubov dispersion relation
\begin{equation*} \varepsilon_{\small Bog} (k) = \left[ k^4 + 4 cn k^2 \right]^{1/2}. \end{equation*}The Hamiltonian itself simplifies to
\begin{equation*} H_{LL}^{\small Bog} = E_0 + \frac{1}{L} \sum_{k\neq 0} \varepsilon_{\small Bog} (k) \tilde{\psi}^\dagger_k \tilde{\psi}_k \end{equation*}where the ground state energy is
\begin{equation*} \frac{E_0}{L} = c n^2 + \int_0^\infty \frac{dk}{2\pi} \left( [k^4 + 4 cn k^2]^{1/2} - k^2 - 2cn \right) = c n^2 - \frac{4}{3\pi} (cn)^{3/2} = n^3 \gamma \left( 1 - \frac{4}{3\pi} \sqrt{\gamma} \right) \end{equation*}in terms of the effective interaction parameter \(\gamma = c/n\).
The Bogoliubov approach should provide an accurate approximation of the Lieb-Liniger model in the limit of small interactions. Note the the ground state energy has non-algebraic corrections in terms of the interaction parameter, reflecting the fact that naive perturbation theory around the noninteracting point fails. Bogoliubov theory cannot be accurate for large interactions, in any case certainly not for \(\gamma > (3\pi/4)^2 \approx 5.55\), where the prediction for the ground state energy becomes negative. A slightly more refined limit is that since the ground-state energy must be a monotonically increasing function of the interaction (this being a simple consequence of the Hellman-Feynman theorem \(\frac{dE_0}{dc} = \langle \frac{dH}{dc} \rangle_0\)), Bogoliubov theory cannot be a valid approximation for the Lieb-Liniger model when \(\gamma > (\pi/2)^2 \approx 2.47\). Of course, how accurate Bogoliubov theory is depends very much on which question is being asked. We will comment on its validity for various quantities at relevant points in our study of the physics of the Lieb-Liniger model.
Solving the Schrödinger equation
The exact solution of the Schrödinger equation for this model was obtained in 1963.Lieb.PR.130.1 1963.Lieb.PR.150.2. We here do things very progressively, starting from the two-particle case.
Two particles
Specializing the Lieb-Liniger Hamiltonian l.h1 to two particles gives the simple Hamiltonian
<<l.h1n2>>
For the moment, we consider that the particles live on the real line, and thus \((x_1, x_2) \in \mathbb{R}^2\). Our interaction parameter \(c\) can for now also take any real value, \(c>0\) representing repulsive interactions, and \(c<0\) attractive ones.
As is familiar from basic quantum mechanics, the contact interaction between the two particles brings about a cusp (discontinuity in the first derivative) in the wavefunction at the point where coordinates coincide. This is most easily expressed by moving to relative coordinates \(x_+ = \frac{x_1 + x_2}{2}, x_- = x_1 - x_2\), integrating l.se1 over a vanishingly small inverval \(x_- = [-\epsilon, \epsilon]\), and taking the limit \(\epsilon \rightarrow 0^+\), yielding the condition
<<l.bc>>
Since we are dealing with bosons, the physical Hilbert space is restricted to completely symmetric functions, meaning that we require \(\Psi_2 (x_1, x_2) = \Psi_2 (x_2, x_1)\). In that case, condition l.bc can be simplified to
<<l.d>>
The wavefunctions thus indeed acquire a jump in their first derivative when relative particle positions change sign, and the size of this jump is the value of the interaction strength \(c\).
In order to display explicit solutions of the Schrödinger equation, two routes can be followed. Namely, one can simply solve l.h1n2 in the whole domain \((x_1, x_2) \in \mathbb{R}^2\) starting from a general enough initial form (Ansatz) for the form of the wavefunctions. Alternately, one can restrict to the fundamental domain
\begin{equation*} D_2: x_1 < x_2, \hspace{10mm} \mbox{with boundary} \hspace{10mm} \partial D_2: x_2 = x_1 + 0^+ \end{equation*}and solve the multivariable boundary value problem
\begin{equation*} \left( H_{\small LL}^{\small (2)} - E_2 \right) \Psi_2 (x_1, x_2) \bigr|_{(x_1, x_2) \in D_2} = 0, \hspace{10mm} \left(\partial_{x_2} - \partial_{x_1} - c \right) \Psi_2 (x_1, x_2) \bigr|_{(x_1, x_2) \in \partial D_2} = 0, \end{equation*}the extension from \(D_2\) to \(\mathbb{R}^2\) being effectuated by invoking the symmetry properties of the wavefunctions under particle exchange.
Let us follow this second route. The projection of the Hamiltonian l.h1n2 to \(D_2\) is then simply the two-particle Laplacian \(-\partial_{x_1}^2 - \partial_{x_2}^2\), which is simply solved in terms of free waves (note: one might also consider a zero mode solution of the form \(\alpha + \beta x\), with constant \(\alpha\) and \(\beta\). The first is excluded by the interaction term; the second, by the boundary conditions (if in finite size) or the normalizability condition (if on the real line)).
Given two generic complex numbers \(\lambda_1, \lambda_2\) representing quasimomenta (postponing until later the discussion of whether these numbers are restricted to the real line or not), one can construct two plane wave solutions
\begin{equation*} e^{i \lambda_1 x_1 + i \lambda_2 x_2} \hspace{5mm} \mbox{and}\hspace{5mm} e^{i \lambda_2 x_1 + i \lambda_1 x_2} \end{equation*}having the same energy and total momentum, namely
\begin{equation*} E_2 = \lambda_1^2 + \lambda_2^2, \hspace{5mm} P_2 = \lambda_1 + \lambda_2. \end{equation*}We thus begin by setting the form
<<l.psi2a>>
for some as yet undetermined complex amplitudes \(S_1, S_2\). Substituting this form in l.d immediately leads to the restriction
<<l.s>>
which must be fulfilled in order to solve the Schrödinger equation on the boundary \(\partial D_2\).
Let us now reconsider the question of whether our quasimomenta can indeed take values in the unrestricted field of complex numbers. From the form of the wavefunction l.psi2a, we can see that we must impose \(\mbox{Im}~ \lambda_i \leq 0\) if we require that \(\Psi_2\) remains finite as we take \(x_1 \rightarrow -\infty\). Similarly, we must impose \(\mbox{Im}~ \lambda_i \geq 0\) if the same is to hold true when we take \(x_2 \rightarrow \infty\). This argumentation of course does not apply to a finite system. We will discuss this `reality' issue in further details later on, assuming for the moment that the quasimomenta are indeed real numbers.
Since the ratio l.s is of the form \(a/a^*\), we can write conveniently it as a phase,
\begin{equation*} \frac{S_2}{S_1} = -e^{i\phi(\lambda_1- \lambda_2)}, \end{equation*}where
<<l.phi>>
This allows us to write our two-particle wavefunction (up to an arbitrary phase, and postponing the question of normalization until later) as
\begin{equation*} \Psi_2^{\small (a)} (x_1, x_2 | \lambda_1, \lambda_2) \bigr|_{(x_1, x_2) \in D_2} = e^{i \lambda_1 x_1 + i \lambda_2 x_2 - \frac{i}{2} \phi(\lambda_1 - \lambda_2)} - e^{i \lambda_2 x_1 + i \lambda_1 x_2 + \frac{i}{2} \phi(\lambda_1 - \lambda_2)}. \end{equation*}The domain of applicability of this form can then simply be extended to the whole domain \((x_1, x_2) \in \mathbb{R}^2\) by invoking complete symmetry under coordinate exchange, yielding the wavefunction
\begin{equation*} \Psi_2^{\small (a)} (x_1, x_2 | \lambda_1, \lambda_2) = sgn(x_2 - x_1)~\left\{e^{i \lambda_1 x_1 + i \lambda_2 x_2 - \frac{i}{2}sgn(x_2 - x_1) \phi(\lambda_1 - \lambda_2)} - e^{i \lambda_2 x_1 + i \lambda_1 x_2 + \frac{i}{2} sgn(x_2 - x_1) \phi(\lambda_1 - \lambda_2)} \right\}, \end{equation*}or more aesthetically
\begin{equation*} \Psi_2^{\small (a)} (x_1, x_2 | \lambda_1, \lambda_2) = sgn(x_2 - x_1) \sum_{P \in \pi_2} (-1)^{[P]} e^{i \lambda_{P_1} x_1 + i \lambda_{P_2} x_2 - i sgn(x_2 - x_1) \phi (\lambda_{P_1} - \lambda_{P_2})/2}. \end{equation*}Here, the summation is over the set \(\pi_2\) of permutations of the set of integers \((1,2)\). This form will be readily generalizable to arbitrary particle numbers, in which case we will call it the Bethe Ansatz.
Note that this wavefunction, manifestly symmetric in coordinates, is manifestly anti-symmetric in quasimomenta:
\begin{equation*} \Psi_2^{\small (a)} (x_1, x_2 | \lambda_1, \lambda_2) = - \Psi_2^{\small (a)} (x_1, x_2 | \lambda_2, \lambda_1). \end{equation*}Wavefunctions for which \(\lambda_1 = \lambda_2\) thus identically vanish and do not represent bona fide eigenstates. This is a manifestation of an underlying Pauli-like principle, which will be determinantal in the classification of eigenstates to be performed later. That said, this antisymmetry under permutation of quasimomenta is artificial, and carries no direct physical meaning. The only real constraint is that the wavefunction forms an irreducible representation of the permutation group of quasimomenta. We can thus just as well choose our wavefunction to be symmetric under quasimomenta exchanges,
\begin{equation*} \Psi_2^{\small (s)} (x_1, x_2 | \lambda_1, \lambda_2) = sgn (\lambda_2 - \lambda_1) \Psi_2^{\small (a)} (x_1, x_2 | \lambda_1, \lambda_2). \end{equation*}This choice will in fact turn out to be more natural in view of our later considerations of the Algebraic Bethe Ansatz. We will thus take our final form for the \(N=2\) wavefunction to be
<<l.psi2>>
As a final comment, one could have found the same wavefunction using the first route mentioned above, starting from the symmetry-inspired Ansatz
<<l.psi2t>>
By applying the differential operator form l.h1, using the properties of the \(\delta\) function, one can directly verify that this is indeed a solution of the time-independent Schrödinger equation l.se1 provided the coefficients \(S_i\) satisfy the constraint l.s.
Verification that l.psi2t solves the Schrödinger equation:
\begin{align*} \partial_{x_1} \Psi_2 (x_1, x_2) = -\delta (x_2 - x_1) (S_1 + S_2) e^{i (\lambda_1 + \lambda_2) x_1} + \delta (x_1 - x_2) (S_1 + S_2) e^{i(\lambda_1 + \lambda_2) x_1} + \nonumber \\ + \theta (x_2 - x_1) \left\{ i\lambda_1 S_1 e^{i \lambda_1 x_1 + i \lambda_2 x_2} + i\lambda_2 S_2 e^{i \lambda_2 x_1 + i \lambda_1 x_2} \right\} + \theta (x_1 - x_2) \left\{ i\lambda_1 S_2 e^{i \lambda_1 x_1 + i \lambda_2 x_2} + i\lambda_2 S_1 e^{i \lambda_2 x_1 + i \lambda_1 x_2} \right\} \nonumber \\ = \theta (x_2 - x_1) \left\{ i\lambda_1 S_1 e^{i \lambda_1 x_1 + i \lambda_2 x_2} + i\lambda_2 S_2 e^{i \lambda_2 x_1 + i \lambda_1 x_2} \right\} + \theta (x_1 - x_2) \left\{ i\lambda_1 S_2 e^{i \lambda_1 x_1 + i \lambda_2 x_2} + i\lambda_2 S_1 e^{i \lambda_2 x_1 + i \lambda_1 x_2} \right\} \end{align*} \begin{align*} -\partial_{x_1}^2 \Psi_2 (x_1, x_2) = \delta (x_1 - x_2) \left\{ i (\lambda_1 - \lambda_2) (S_1 - S_2) e^{i (\lambda_1 + \lambda_2) x_1} \right\} + \nonumber \\ + \theta (x_2 - x_1) \left\{ \lambda_1^2 S_1 e^{i \lambda_1 x_1 + i \lambda_2 x_2} + \lambda_2^2 S_2 e^{i \lambda_2 x_1 + i \lambda_1 x_2} \right\} + \nonumber \\ + \theta (x_1 - x_2) \left\{ \lambda_1^2 S_2 e^{i \lambda_1 x_1 + i \lambda_2 x_2} + \lambda_2^2 S_1 e^{i \lambda_2 x_1 + i \lambda_1 x_2} \right\} \end{align*}Many particles
The above considerations for two particles readily generalize to the case of an arbitrary number of particles. One defines a fundamental open domain
\begin{equation*} D_N: x_1 < x_2 < ... < x_N \hspace{10mm} \mbox{with boundaries} \hspace{10mm} \partial_j D_N: x_{j+1} = x_j + 0^+, \end{equation*}the solution of the time-independent Schrödinger equation l.se1 being equivalent to the solution of the system
\begin{equation*} \left( H_{\small LL}^{\small (N)} - E_N \right) \Psi_N ({\bf x}) \bigr|_{{\bf x} \in D_N} = 0, \hspace{10mm} \left(\partial_{x_{j+1}} - \partial_{x_j} - c \right) \Psi_N ({\bf x}) \bigr|_{{\bf x} \in \partial_j D_N} = 0. \end{equation*}If we consider the region of \(\mathbb{R}^N\) in which at most two coordinates exactly coincide, the full \(N\)-body wavefunction is given by a straightforward generalization of the two-body result l.psi2,
<<l.psin>>
The Bethe wavefunction thus has four distinctive features:
- it is a mixture of plane waves,
- each plane waves carrying a rapidity (internal quasi-momentum) label,
- these plane waves are combined using relative amplitudes set by microscopic two-body interactions
- the internal quasi-momenta obey a form of Pauli exclusion (since the wavefunction identically vanishes in the case of pairwise equal rapidities, as direct inspection reveals).
Quantization and the Bethe equations
Until now, we have considered our system as being defined on the whole real line. The disadvantage of this is that considering a finite particle number \(N\) then only allows to access the zero-density case. As in many standard problems of quantum mechanics, in order to classify states, it is more reasonable to introduce a finite quantization length. We will thus put our system on an interval of length \(L\) and impose for now simple periodic boundary conditions on the wavefunctions.
Two particles
Let us start again from the \(N=2\) case, which illustrates the general construction. The periodicity conditions can be written as
\begin{equation*} \Psi_2 (x_1 + L, x_2| \lambda_1, \lambda_2) = \Psi_2 (x_1, x_2 + L| \lambda_1, \lambda_2) = \Psi_2 (x_1, x_2| \lambda_1, \lambda_2). \end{equation*}Looking at l.psi2 and invoking the linear independence of the free waves with distinct rapidities gives the following quantization conditions for the rapidities:
\begin{equation*} e^{i\lambda_1 L} = - e^{-i \phi (\lambda_1, \lambda_2)}, \hspace{1cm} e^{i \lambda_2 L} = - e^{i \phi(\lambda_1, \lambda_2)}, \end{equation*}which can also be rewritten using l.phi as
\begin{equation*} e^{i \lambda_1 L} = \frac{\lambda_1 - \lambda_2 + ic}{\lambda_1 - \lambda_2 - ic}, \hspace{10mm} e^{i \lambda_2 L} = \frac{\lambda_2 - \lambda_1 + ic}{\lambda_2 - \lambda_1 - ic}. \end{equation*}These are known as Bethe equations. In view of the state classification, their most convenient form is obtained by taking the logarithm,
\begin{equation*} \lambda_1 + \frac{1}{L} \phi (\lambda_1 - \lambda_2) = \frac{2\pi}{L} I_1, \hspace{1cm} \lambda_2 + \frac{1}{L} \phi (\lambda_2 - \lambda_1) = \frac{2\pi}{L} I_2, \end{equation*}where
\begin{equation*} I_1, I_2 \in \mathbb{Z} + \frac{1}{2} \end{equation*}are half-odd integers uniquely labelling the quasimomenta \(\lambda_1, \lambda_2\), and thus take the role of quantum numbers of the theory. Subtracting the two equations,
\begin{equation*} \lambda_1 - \lambda_2 + \frac{2}{L}\phi (\lambda_1 - \lambda_2) = \frac{2\pi}{L} (I_1 - I_2), \end{equation*}and using the monotonicity of the phase shift function l.phi shows that the sign of \(I_1 - I_2\) is the same as that of \(\lambda_1 - \lambda_2\). Therefore, if \(I_1 = I_2\), we must have \(\lambda_1 = \lambda_2\). In this case however, as we have seen, the wavefunction identically vanishes, manifesting the Pauli principle for the Bethe Ansatz.
The total momentum and energy of this two-particle wavefunction are simply
\begin{equation*} P = \lambda_1 + \lambda_2, \hspace{10mm} E = \lambda_1^2 + \lambda_2^2. \end{equation*}Many particles
The above considerations generalize to an arbitrary number \(N\) of particles. The periodicity conditions are then
\begin{equation*} \Psi_N (x_1, ..., x_{j-1}, x_j + L, x_{j+1}, ..., x_N | {\boldsymbol \lambda} ) = \Psi_{N} (x_1, ..., x_{j-1}, x_j, x_{j+1}, ..., x_N | {\boldsymbol \lambda} ). \end{equation*}Imposing these in l.psin immediately leads to the Bethe equations (using \(\phi (0) = 0\))
\begin{equation*} e^{i\lambda_j L} = (-1)^{N-1} e^{-i \sum_{l=1}^N \phi (\lambda_j - \lambda_l)} \end{equation*}which explicitly written out are
<<l.be>>
or in logarithmic form
<<l.bel>>
where
<<l.i>>
are again quantum numbers labelling the eigenstates, whose total momentum and energy are
<<l.pe>>
At this point, we are thus in position to conjecture that a complete set of wavefunctions is obtained by choosing all allowable sets of non-coincident quantum numbers and constructing their associated Bethe Ansatz wavefunctions.
Properties of solutions to the Bethe equations
<<l.th1>>
Theorem 1: all solutions of the Bethe equations for the interacting Bose gas are real for \(c > 0\).
Proof: consider \(e^{i \lambda L}\). Observe that \(|e^{i\lambda L}| \leq 1\) for \(\mbox{Im}~ \lambda \geq 0\) and \(|e^{i\lambda L}| \geq 1\) for \(\mbox{Im}~ \lambda \leq 0\). Moreover, \(|(\lambda + ic)/(\lambda-ic)| \geq 1\) for \(\mbox{Im}~ \lambda \geq 0\) and \(c > 0\), and then also \(|(\lambda + ic)/(\lambda-ic)| \leq 1\) for \(\mbox{Im}~ \lambda \leq 0\).
Consider a set \(\{ \lambda_j \}\), \(j = 1, ..., N\), solution to the Bethe equations for a given proper set of quantum numbers \(\{ I_j \}\). Define the momentum with maximal imaginary part \(\lambda_{max} \in \{ \lambda_j \}\), such that \(\mbox{Im}~ \lambda_{max} \geq \mbox{Im}~ \lambda_j\), \(j = 1, ..., N\). The Bethe equation for \(\lambda_{max}\) gives
\begin{equation*} |e^{i\lambda_{max} L} | = \left| \prod_j \frac{\lambda_{max} - \lambda_j + ic}{\lambda_{max} - \lambda_j - ic} \right| \geq 1 \end{equation*}meaning that we must have \(\mbox{Im}~ \lambda_{max} \leq 0\), so \(\mbox{Im}~ \lambda_j \leq 0 ~\forall ~j\). Defining \(\lambda_{min}\) in a similar way, we can show that \(\mbox{Im}~ \lambda_j \geq 0 ~\forall ~j\), so \(\mbox{Im}~ \lambda_j = 0 ~\forall ~j\) \(\Box\).
<<l.th2>>
Theorem 2: for \(c > 0\) and for a given proper set of quantum numbers \(\{ I_j\}\), the solution for the set \(\{ \lambda_j \}\) exists and is unique (Yang and Yang '69 1969.Yang.JMP.10).
Proof: The Bethe equations are equivalent to the extremum conditions for the so-called Yang-Yang action
<<l.yya>>
where
\begin{equation*} \Phi (\lambda) = \int_0^\lambda d\lambda' \phi (\lambda') = 2\lambda ~\mbox{atan}~ \frac{\lambda}{c} - c \ln (1 + \lambda^2/c^2). \end{equation*}That is, equating
\begin{equation*} \partial_{\lambda_j} S (\{ \lambda \}) = \lambda_j L + \sum_l \phi (\lambda_j - \lambda_l) - 2\pi I_j \end{equation*}to zero for all directions yields the set of Bethe equations.
Consider now the Hessian of the Yang-Yang action, namely the matrix of second-order derivatives
\begin{align*} S_{jl} \equiv \frac{\partial^2 S}{\partial_{\lambda_j} \partial_{\lambda_l}} &= \partial_{\lambda_j} \left\{\lambda_l L + \sum_{m \neq l} 2~\mbox{atan}~ \frac{\lambda_l - \lambda_m}{c} - 2\pi I_l \right\} \nonumber \\ &= \delta_{jl} \left\{ L + \sum_{m=1}^N \frac{2c}{(\lambda_j - \lambda_m)^2 + c^2} \right\} - \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2} \end{align*}For any real vector \({\bf v}\) with nonzero norm, we can build the quadratic form
\begin{align*} \sum_{j,l} v_j S_{jl} v_l &= \sum_{j=1}^N v_j^2 L + \sum_{j,m=1}^N v_j^2 \frac{2c}{(\lambda_j - \lambda_m)^2 + c^2} - \sum_{j,l=1}^N v_j v_l \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2} \nonumber \\ &= \left.\sum_{j=1}^N v_j^2 L + \sum_{j>l=1}^N (v_j - v_l)^2 \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2}\right|_{c > 0} > 0. ~~~~~ \end{align*}Thus, \(S\) is a strictly concave function in \(N\)-dimensional space, and the solution to the extremum condition (the Bethe equations) for a given proper set of quantum numbers is unique \(\Box\).
<<l.th3>>
Theorem 3: for \(c > 0\), if \(I_j > I_l\) then \(\lambda_j > \lambda_l\). If \(I_j = I_l\) then \(\lambda_j = \lambda_l\).
Proof: subtracting the Bethe equation for \(\lambda_l\) from that for \(\lambda_j\) gives
<<l.ld>>
Since the \(\phi\) kernel is monotonic, the first and second terms on the left-hand side of this equation have the same sign, directly proving the theorem.
<<l.th4>>
Theorem 4: for \(c > 0\), the rapidity differences are bounded by
<<l.bd>>
Proof: defining the Cauchy kernel
<<l.ck>>
we note that
\begin{equation*} 0 \leq {\cal C} (\lambda) \leq \frac{1}{\pi c}, \hspace{10mm} \lambda \in \mathbb{R} \end{equation*}and thus that
\begin{equation*} \phi (\lambda_1) - \phi (\lambda_2) = 2\pi \int_{\lambda_2}^{\lambda_1} d\lambda ~{\cal C} (\lambda) \leq \frac{2}{c} (\lambda_1 - \lambda_2). \end{equation*}Substituting this in equation l.ld then immediately completes the proof.
Norms of Bethe eigenstates: Gaudin's conjecture
Computing the norm of Bethe eigenstates seems difficult, since the wavefunctions are made up of factorially many terms. In fact, this illustrates the general difficulties encountered when attempting to calculate anything starting from the explicit Bethe Ansatz expression for the wavefunctions. Let's go back to the two-particle case, and consider the wavefunction
\begin{equation*} \Psi_2 (x_1, x_2| \lambda_1, \lambda_2)|_{0 \leq x_1 < x_2 \leq L} = e^{i\lambda_1 x_1 + i\lambda_2 x_2 -\frac{i}{2} \phi(\lambda_1, \lambda_2)} - e^{i\lambda_2 x_1 + i\lambda_1 x_2 +\frac{i}{2} \phi(\lambda_1, \lambda_2)}. \end{equation*}Let's compute the norm of this in the domain \(0 \leq x_1 < x_2 \leq L\):
\begin{equation*} {\mathbb N}_2 = \int_0^L dx_1 \int_{x_1}^L dx_2 | \Psi_2|^2 = I_1 - 2 \Re I_2 \end{equation*}where
\begin{equation*} I_1 = 2 \int_0^L dx_1 \int_{x_1}^L dx_2 = L^2 \end{equation*}and (using the notation \(\lambda_{12} \equiv \lambda_1 - \lambda_2\))
\begin{equation*} I_2 = \int_0^L dx_1 \int_{x_1}^L dx_2 e^{i\lambda_{12} x_{12} -i\phi_{12}} = \frac{e^{-i\phi_{12}}}{\lambda_{12}} \left[ \frac{1 - e^{-i\lambda_{12}L}}{\lambda_{12}} - iL\right]. \end{equation*}From the Bethe equations, we get that \(e^{-i\lambda_{12}L} = e^{2i\phi_{12}}\) so (making use of the definition of \(\phi_{12}\)) we get
\begin{equation*} 2\Re I_2 = -\frac{L}{\lambda_{12}} 2\sin \phi_{12} = -\frac{L}{\lambda_{12}} \frac{4c \lambda_{12}}{\lambda_{12}^2 + c^2} = -\frac{4cL}{\lambda_{12}^2 + c^2} \end{equation*}Therefore, the square norm of the two-particle state is
\begin{equation*} {\mathbb N}_2 = L^2 + \frac{4cL}{\lambda_{12}^2 + c^2} \end{equation*}This coincides with the following determinant:
\begin{equation*} \left| \begin{array}{cc} L + \frac{2c}{\lambda_{12}^2 + c^2} & \frac{-2c}{\lambda_{12}^2 + c^2} \\ \frac{-2c}{\lambda_{12}^2 + c^2} & L + \frac{2c}{\lambda_{12}^2 + c^2} \end{array} \right| = ~\mbox{det} \left(\frac{\partial^2 S}{\partial_{\lambda_j} \partial_{\lambda_l}}\right). \end{equation*}That is, for two particles in the Bose gas, the square norm of the wavefunction coincides with the determinant of the Hessian matrix of the Yang-Yang action (we will call this matrix the Gaudin matrix from now on).
Amazingly, this results also holds for higher particle numbers,
\begin{equation*} {\mathbb N}_{N} = ~\mbox{det}_N \left(\frac{\partial^2 S}{\partial_{\lambda_j} \partial_{\lambda_l}}\right). \end{equation*}This result, first conjectured by M. Gaudin b-Gaudin based on the corresponding infinite-size formulas 1971.Gaudin.JMP.12.I 1971.Gaudin.JMP.12.II, was proved by V. Korepin using the Algebraic Bethe Ansatz in 1982.Korepin.CMP.86. This determinant is also the Jacobian of the transformation of variables from the rapidities \(\lambda\) to the quantum numbers \(I\), \(\frac{D(\lambda_1, ..., \lambda_N)}{D(I_1, ..., I_N)}\). Since the measure for state summation in quantum number space is completely flat, it is not surprising that the norm of the state should correspond to such a Jacobian.
Since it really only relies on the form of the Bethe Ansatz wavefunction, Gaudin's formula also holds true for other integrable models. In particular, for spin chains, the square norm of Bethe eigenstates is given by the determinant of the appropriate Gaudin matrix.
The Heisenberg spin-\(1/2\) chain
Quantum spin chains represent one of the most useful settings in which to investigate many-body quantum physics. We here restrict to the simplest case of spin-\(1/2\), which is the furthest away from the classical limit. The isotropic Heisenberg model is considered in detail, and its anisotropic generalizations are covered in later sections.
In this section, we construct the eigenfunctions of finite (anisotropic) Heisenberg magnets using the coordinate Bethe Ansatz.
Definitions
The Hamiltonian of the Heisenberg magnet which we will use throughout is
<<xxz.h>>
\(J\) is the exchange coupling, with \(J > 0\) (resp. \(J < 0\)) being the antiferromagnetic (resp. ferromagnetic) case. The parameter \(\Delta \in {\mathbb R}\) is called the anisotropy of the model. The spin-\(1/2\) operators \(S^{\alpha}_j\) are equipped with indices \(\alpha = x, y, z\) and \(j\) which labels the lattice site. We consider a closed periodic chain, so that
<<xxz.pbc>>
These operators obey canonical \(su(2)\) commutation relations
\begin{equation*} \left[ S^{\alpha}_j, S^{\beta}_k \right] = i \hbar \delta_{jk} \epsilon^{\alpha \beta \gamma} S^{\gamma}_j \end{equation*}where \(\epsilon^{\alpha \beta \gamma}\) is the completely antisymmetric tensor, and the Kronecker symbol \(\delta_{jk}\) ensures commutation of operators on different sites. More convenient operators for calculations are the spin raising and lowering operators
\begin{equation*} S^{\pm}_j = S^x_j \pm i S^y_j \end{equation*}with commutation relations
\begin{equation*} \left[S^z_j, S^{\pm}_k \right] %= \left[ S^z_j, S^x_k \pm i S^y_k \right] = \pm \hbar \delta_{jk} S^{\pm}_j, \hspace{1cm} \left[ S^+_j, S^-_k \right] = 2\hbar \delta_{jk} S^z_j. \end{equation*}These provide an equivalent form of xxz.h,
<<xxz.hp>>
Most of our review will concern the spin-\(1/2\) chain, for which the spin operators can be represented using Pauli spin matrices,
\begin{equation*} S^{\alpha}_j = \frac{\hbar}{2} \sigma^{\alpha}_j, \end{equation*}with the standard definitions used for each site
\begin{equation*} \sigma^x = \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), \hspace{1cm} \sigma^y = \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array} \right), \hspace{1cm} \sigma^z = \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right). \end{equation*}The Pauli ladder operators are defined as
\begin{equation*} \sigma^+ = \frac{\sigma^x + i \sigma^y}{2} = \left(\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array} \right) \equiv S^+, \hspace{1cm} \sigma^- = \frac{\sigma^x - i \sigma^y}{2} = \left(\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array} \right) \equiv S^-. \end{equation*}The Hilbert space \({\cal H}_j\) on each lattice site \(j\) is then spanned by the two states \(| \pm \rangle_j\), chosen as eigenstates of the \(S^z_j\) operator (N.B.: from now on, we take \(\hbar = 1\)):
\begin{equation*} S^z_j | \pm \rangle_j = \pm \frac{1}{2} | \pm \rangle_j, \hspace{1cm} S^{\pm}_j | \mp \rangle_j = | \pm \rangle_j, \hspace{1cm} S^{\pm}_j | \pm \rangle_j = 0. \end{equation*}The full Hilbert space is obtained by tensoring all the on-site spaces, \({\cal H} = \oplus_{j=1}^N {\cal H}_j\). It is spanned by the set of \(2^N\) basis states \(\{ | \epsilon_1, ..., \epsilon_N \rangle \}\) with \(\epsilon_j = \{ +, -\} ~\forall j\). One particular member of this set will be of importance later on: the state with all spins pointing up along \(\hat{z}\),
<<xxz.r>>
We will refer to this state as the reference state.
The \(XXZ\) Hamiltonian xxz.h commutes with the \(\hat{z}\)-projection of the total spin operator, \(S^z_{\rm tot} = \sum_{j=1}^N S^z_j\), \[ \left[ H, S^z_{\rm tot} \right] = 0, \] so that the Hilbert space separates into subspaces of fixed magnetization along the \(\hat{z}\) axis. We label each of these subspaces \({\cal H}_M\) by the integer \(M \in \{0, 1, ..., N \}\) representing the number of down spins, i.e. \(S^z_{\rm tot} = \frac{N}{2} - M\). The dimensionality of each subspace is then given by the binomial coefficient \(\mbox{dim} ({\cal H}_M) = \left( \begin{array}{c} N \\ M \end{array} \right)\), fulfilling the requirement \(\sum_{M = 0}^N \mbox{dim} ({\cal H}_M) = 2^N\).
Solving the Schrödinger equation
Let us now construct the eigenstates of the \(XXZ\) Hamiltonian xxz.h (or the equivalent xxz.hp). We proceed sector by sector in magnetization.
0 down spins
The fully (up) polarized sector is trivial: \(S^z_{\rm tot} = \frac{N}{2}\), and this sub-Hilbert space is spanned by the single state xxz.r of zero energy, \(H |0 \rangle = 0\).
1 down spin
Only slightly less trivial is the \(M = 1\) subsector. Let us use the Ansatz \(|\Psi_1 \rangle = \sum_{j=1}^N \Psi_1 (j) | j \rangle\) in which \(| j \rangle = S^-_j | 0 \rangle\) and \(\Psi_1 (j + N) = \Psi_1 (j)\) to ensure periodicity. Projecting the Schrödinger equation \(H |\Psi_1 \rangle = E_1 |\Psi_1 \rangle\) onto the bra \(\langle j |\) yields the conditions \[ \frac{J}{2} \left(\Psi_1 (j - 1) + \Psi_1 (j + 1)\right) = (E_1 + J\Delta) \Psi_1 (j), \] which are solved by the free wave Ansatz \(\Psi_1(j) = e^{i k j}\) provided the energy is
\begin{equation*} E_1 = J (\cos k -\Delta). \end{equation*}Periodicity quantizes the momentum according to \(e^{ikN} = 1\). The allowed values of momentum are therefore given by
\begin{equation*} k = 2\pi \tilde{I}/N, \hspace{1cm} \tilde{I} = 0, 1, ..., N - 1 \end{equation*}(or any equivalent coverage of the Brillouin zone). For lattice size \(N\), there are thus \(N\) linearly independent solutions, a number corresponding to the Hilbert space dimensionality \(\left( \begin{array}{c} N \\ 1 \end{array} \right) = N\). This simple Ansatz therefore generates all the wavefunctions in this subspace.
2 down spins
The \(M = 2\) subsector is less trivial, but provides the necessary building blocks for generalization to arbitrary \(M \leq \frac{N}{2}\). We look for an eigenstate of the form \(| \Psi_2 \rangle = \sum_{j_1 < j_2} \Psi_2 (j_1, j_2) | j_1, j_2 \rangle\) where \(|j_1, j_2\rangle = S^-_{j_1} S^-_{j_2} |0\rangle\). Projecting the Schrödinger equation onto the bra \(\langle j_1, j_2|\) yields the bulk conditions (note that \(| j_1, j_2 \rangle\) is identically zero for \(j_1 = j_2\) mod \(N\), so \(\Psi(j, j)\) can actually be chosen arbitrarily)
<<xxz.se>>
To solve these, we generalize the \(M = 1\) case and look for a wavefunction in the form of a free wave Ansatz,
<<xxz.psi2>>
The equation for \(j_1 + 1 < j_2\) gives
\begin{equation*} E_2 = J(\cos k_1 + \cos k_2 - 2\Delta). \end{equation*}The second equation then yields \[ \frac{A_{21}}{A_{12}} = - \frac{1 + e^{i (k_1 + k_2) } - 2\Delta e^{i k_2}}{1 + e^{i (k_1 + k_2)} - 2\Delta e^{i k_1}} \equiv -e^{i\phi(k_1, k_2)} \] where we have defined the scattering phase shift function
<<xxz.phi>>
which will play an immensely important role in the following. Using the phase shift function, the (unnormalized) trial wavefunction can now be written
\begin{equation*} \Psi_2 (j_1, j_2) = e^{i k_1 j_1 + i k_2 j_2 - \frac{i}{2} \phi(k_1, k_2)} - e^{i k_2 j_1 + i k_1 j_2 + \frac{i}{2} \phi(k_1, k_2)}. \end{equation*}We do not have our eigenstates yet: in addition to the bulk conditions xxz.se, there are also four equations of boundary type which are equivalent to the periodicity conditions
\begin{equation*} \Psi_2(j_2, j_1 + N) = \Psi_2 (j_1, j_2), \hspace{1cm} \Psi_2(j_2 - N, j_1) = \Psi_2 (j_1, j_2). \end{equation*}These conditions yield the so-called Bethe equations, constraining the allowed values of the bare momenta \(k_i\):
\begin{equation*} e^{i k_1 N} = - e^{-i \phi(k_1, k_2)}, \hspace{1cm} e^{i k_2 N} = -e^{+i \phi(k_1, k_2)}. \end{equation*}For classifying the solutions, it is more conveninent (as was done for \(M = 1\)) to take the logarithm:
\begin{equation*} N k_1 + \phi (k_1, k_2) = 2\pi \tilde{I}_1, \hspace{1cm} N k_2 - \phi(k_1, k_2) = 2\pi \tilde{I}_2 \end{equation*}where \(\tilde{I}\) are half-odd integers.
General \(M\)
For \(XXZ\) with \(M \leq N/2\) down spins, the Bethe Ansatz reads
<<xxz.ba>>
where the two-particle scattering phase shift is given by xxz.phi. This is an eigenstate provided the bare momenta \(k_a\) fulfill the set of \(M\) coupled Bethe equations
<<xxz.be>>
or in logarithmic form,
<<xxz.bel>>
where \(\tilde{I}_a\) are half-odd integers if \(M\) is even, and integers if \(M\) is odd.
The energy and momentum of such an eigenstate are
<<xxz.ep>>
The physics of Bethe Ansatz-solvable spin-\(1/2\) chains depends crucially on the value of the anisotropy parameter \(\Delta\). We begin by a thorough examination of the most important case, namely the isotropic antiferromagnet case with \(\Delta = 1\).
Parametrization in terms of rapidities
Let us now specialize to the most important case of the isotropic antiferromagnet (\(\Delta = 1\)).
The bare momenta \(k_a\) will be parametrized in terms of rapidities \(\lambda\) according to
<<h.l>>
such that \(k(\lambda = 0) = \pi\). Such a parametrization is purposefully chosen to make the scattering phase shift become a new function depending only on the rapidity difference, namely \(\phi(k_1, k_2) \equiv \phi (\lambda_1 - \lambda_2)\) where
\begin{equation*} \phi (\lambda) = 2~\mbox{atan} \lambda. \end{equation*}The Bethe equations for the \(XXX\) model are written in terms of rapidities as
<<h.be>>
or, in logarithmic form,
<<h.bel>>
where the quantum numbers \(I_j\) are half-odd integers for \(N - M\) even, integers for \(N - M\) odd (with \(I_j\) defined mod\((N)\)). For convenience, we have introduced the functions
<<h.phin>>
The energy of a state is given as a function of the rapidities by
<<h.e>>
whereas the momentum has a simple representation in terms of the quantum numbers,
<<h.p>>
Eigenstates of the XXX antiferromagnet
Ground state of the XXX antiferromagnet
The ground state is given by \(I_j^0 = -\frac{M+1}{2} + j\), \(j = 1, ...,M\), and all excited states are obtained (at least in principle) from the different choices of sets \(\{ I_j \}\).
States with real rapidities
Allowable quantum numbers
Consider looking for set of real rapidities as solution to h.bel. The maximally allowed quantum number \(I^{1,\infty}_M\) associated to a rapidity \(\lambda_a \rightarrow \infty\) in the presence of \(M - 1\) other finite rapidities \(\lambda_b < \infty\) is given by taking the limit \[ \lim_{\lambda_a \rightarrow \infty} 2 ~\mbox{atan}~ 2\lambda_a - \frac{1}{N} \sum_{b=1}^{M} 2~\mbox{atan} ~(\lambda_a - \lambda_b) = \pi (1 - \frac{M-1}{N}) \equiv 2\pi \frac{I^{1,\infty}_M}{N} \] from which we get
<<h.im>>
The Bethe equations will therefore have a solution in terms of a set of distinct real, finite rapidities if and only if all quantum numbers obey the inequality \(|I_j| < I^{\infty}_M\).
For a given \(M\), there are thus
\begin{equation*} \left( \begin{array}{c} N - M \\ M \end{array} \right) \end{equation*}states containing exclusively real, finite rapidities. Since the \(XXX\) chain has a global \(su(2)\) symmetry, its eigenstates can be classified according to the representation of this algebra. Eigenstates containing real, finite rapidities only are highest-weight states of this representation b-Gaudin. Acting with the global spin lowering operator to obtain the other non-highest-weight states is achieved by adding infinite rapidities to a state, which still provides a {\it bona fide} solution to the Bethe equations for the XXX chain. At each value of \(M\), it is possible to add up to \(N/2 - M\) infinite rapidities without crossing the equator. We will denote the number of one-strings as \(M_1\), the number of finite-rapidity one-strings as \(M_1^<\) and the number of infinite rapidities as \(M_1^\infty\), so \(M_1 = M_1^< + M_1^\infty\). From the states with purely real, finite rapidities at a fixed \(M\), we can thus construct
\begin{equation*} \sum_{M_1^\infty=0}^{N/2-M} \left( \begin{array}{c} N-M+M_1^\infty \\ M - M_1^\infty \end{array} \right) \end{equation*}states which, for a given \(M_1^\infty\) have global \(su(2)\) quantum numbers \(S = N/2-M+M_1^\infty\), \(S^z = N/2 - M\). Let us provide the simplest examples of these.
\(S = 0\), \(S^z = 0\) sector
For the particular case of zero magnetic field, we have (for \(N\) even) that the magnetization is zero, so \(M = N/2 = M_1\), \(M_1^\infty = 0\). In this case, the ground state is given by the set of quantum numbers
\begin{equation*} \left\{ -\frac{M-1}{2}, -\frac{M-1}{2} + 1, ..., \frac{M-1}{2} \right\} = \left\{ -\frac{N}{4} + \frac{1}{2}, ..., \frac{N}{4} - \frac{1}{2} \right\}. \end{equation*}Since in this case \(I^{\infty}_{N/2} = \frac{N}{4} + \frac{1}{2}\), we see that the {\it only} eigenstate with real, finite rapidities at zero magnetization is the ground state.
\(S = 1\), \(S^z = 1\) sector
We simply have \(M_1 = N/2-1\), \(M_1^\infty = 0\). We have \(I^{1,\infty} = \frac{N}{4} + 1\) and \(I^{\mbox{max}} = \frac{N}{4}\). The number of states is thus \(\left( \begin{array}{c} N/2 + 1 \\ N/2 - 1 \end{array} \right) = \frac{N(N+2)}{8}\). These are the \(S = 1\), \(S^z = 1\) two-spinon states.
\(S = 1\), \(S^z = 0\) sector
Here, we put \(M = N/2 = M_1\), \(M_1^< = N/2-1\) and \(M_1^\infty = 1\). The equations for the limiting quantum numbers then fall back onto the \(M \rightarrow M - 1\) ones, so now \(I^{1,\infty} = \frac{N}{4} + 1\) and \(I^{1,\mbox{max}} = \frac{N}{4}\). We thus have to put \(M_1^<\) quantum numbers in \(N/2 + 1\) slots, yielding \(\left( \begin{array}{c} N/2 + 1 \\ N/2 - 1 \end{array} \right) = \frac{N(N+2)}{8}\) states, which are the \(S = 1, S^z = 0\) two-spinon states.
\(S = 2\), \(S^z = 2\) sector
We simply have \(M = N/2-2 = M_1^<\) finite rapidity one-strings. We have \(I^{1,\infty} = \frac{N}{4} + \frac{3}{2}\) and \(I^{\mbox{max}} = \frac{N}{4} + \frac{1}{2}\). The number of states is thus \(\left( \begin{array}{c} N/2 + 2 \\ N/2 - 2 \end{array} \right) = \frac{(N+4) (N+2) N(N-2)}{384}\). These are the \(S = 2\), \(S^z = 2\) four-spinon states.
\(S = 2\), \(S^z = 1\) sector
We put \(M_1^< = N/2 -2\), \(M_1^\infty = 1\). The equations for the limiting quantum number fall back onto the \(M \rightarrow M-1\) ones. The limiting quantum numbers are \(I^{1,\infty} = \frac{N}{4} + \frac{3}{2}\) so \(I^{\mbox{max}} = \frac{N}{4} + \frac{1}{2}\), so we have to put \(N/2 - 2\) quantum numbers in \(N/2 + 2\) slots, yielding \(\frac{(N+4) (N+2) N (N-2)}{384}\) states, which are the four-spinon states in this sector.
\(S = 2\), \(S^z = 0\) sector
Here, we put \(M_1^< = N/2-2\) and \(M_1^\infty = 2\). The equations for the limiting quantum numbers of the one-string fall back onto the \(M \rightarrow M-2\) ones, so now \(I^{1,\infty} = \frac{N}{4} + \frac{3}{2}\) and \(I^{\mbox{max}} = \frac{N}{4} + \frac{1}{2}\). We thus have to put \(N/2-2\) quantum numbers in \(N/2 + 2\) slots, yielding \(\left( \begin{array}{c} N/2 + 2 \\ N/2 - 2 \end{array} \right) = \frac{(N+4) (N+2) N (N-2)}{384}\) states, which are the four-spinon states in this sector.
Note that for a given \(S\), the number of states at any \(S^z\) is the same due to the invariance of counting under the simultaneous shift \(M \rightarrow M-1\), \(M_1^\infty \rightarrow M_1^\infty + 1\).
String states
The Bethe equations for the \(XXX\) magnet allow solutions which are not restricted to the real line. Complex rapidities can occur. These complex rapidities organize themselves into self-conjugate patterns called {\it strings}, rapidities within an \(n\)-string being reparametrized as
<<h.ls>>
The real parameter \(\lambda_\alpha^j\) represents the {\it string center}, namely the `center of mass' of the composite object represented by the \(n\) rapidities. The string deviations \(\delta_\alpha^{j,a}\) are in most circumstances exponentially small in system size, and can typically be neglected (there are important exceptions to this rule). Since complex rapidities represent bound states of downturned spins (as can be seen from the Bethe Ansatz wavefunction itself), a cluster of the form h.ls represents a single bona fide particle. Out of \(n\) rapidities within a string, we thus get only one independent parameter, the string center \(\lambda_\alpha^{j}\).
The string hypothesis assumes that eigenstates of the Heisenberg chain are represented by sets of rapidities which organize themselves into (perfect) strings. An eigenstate with \(M\) down spins is then understood as an eigenstate with \(M_j\) strings of length \(j\), the total number of downturned spins obeying
\begin{equation*} \sum_{j=1}^\infty j M_j = M. \end{equation*}The total number of strings in an eigenstate is given by
\begin{equation*} \sum_{j=1}^\infty M_j \equiv N_s. \end{equation*}In a given eigenstate, the number of independent parameters is thus \(N_s\) (the number of string centers) instead of \(M\). The Bethe equations for strings can be rewritten by taking the product of h.be over all rapidities within a string. Doing this, one finds (for \(N\) even) the reduced set of Bethe equations
<<h.bgt>>
where
<<h.eE>>
Taking logs, we obtain the following reduced set of equations (which we shall call the Bethe-Gaudin-Takahashi equations)
<<h.bgtl>>
in which
\begin{equation*} I_\alpha^j \in \left\{ \begin{array}{cc} \mathbb{Z} + \frac{1}{2}, & M_j ~\mbox{even} \\ \mathbb{Z}, & M_j ~\mbox{odd}. \end{array} \right. \end{equation*}The kernels \(\phi_j\) are defined as
\begin{equation*} \phi_j(\lambda) = 2\mbox{atan} \frac{2\lambda}{n} \end{equation*}and the string-string scattering phase shift is
<<h.phijk>>
These have the simple limits
\begin{equation*} \lim_{\lambda \rightarrow \infty} \phi_j (\lambda) = \pi, \hspace{10mm} \lim_{\lambda \rightarrow \infty} \Phi_{jk} (\lambda) = (2\min(j,k) - \delta_{jk}) \pi. \end{equation*}Limiting quantum numbers
As for real rapidities, the quantum numbers of strings are limited. We can calculate the maximal string quantum numbers using the same arguments as before:
\begin{equation*} \lim_{\lambda^j_\alpha \rightarrow \infty} (LHS ~\mbox{h.bgtl}) = \frac{2\pi}{N} \frac{1}{2}\left( N - \sum_{k=1}^{N_s} (2\min(j,k) - \delta_{jk}) (M_k - \delta_{jk}) \right) \equiv \frac{2\pi}{N} I^{j,\infty}. \end{equation*}More precisely, this can be rewritten as
\begin{equation*} I^{j,\infty} = \frac{1}{2}\left( N + 2j-1 - \sum_{k=1}^{N_s} (2\min(j,k) - \delta_{jk}) M_k \right). \end{equation*}We will make use of this in the following, in order to classify and count eigenstates.
One two-string
We here take \(M_1 = M - 2\), \(M_2 = 1\). For the one-strings, the limiting quantum numbers become
\begin{align*} \lim_{\lambda^1_{M-2} \rightarrow \infty} \phi_1 (\lambda^1_{M-2}) - \frac{1}{N} \sum_{\alpha = 1}^{M-2} \Phi_{11} (\lambda^1_{M-2} - \lambda^1_\alpha) - \frac{1}{N} \Phi_{12} (\lambda^1_{M-2} - \lambda^2_1) \nonumber \\ = \pi (1 - \frac{M-3}{N} - \frac{2}{N}) \equiv \frac{2\pi}{N} I^{1,\infty}. \end{align*}Similarly, for the two-strings,
\begin{equation*} \lim_{\lambda^2_1 \rightarrow \infty} \phi_2 (\lambda^2_1) - \frac{1}{N} \sum_{\alpha = 1}^{M-2} \Phi_{21} (\lambda^2_1 - \lambda^1_\alpha) = \pi (1 - 2\frac{M-2}{N}) \equiv \frac{2\pi}{N} I^{2,\infty}. \end{equation*}We thus find
\begin{equation*} I^{1,\infty} = \frac{N - M + 1}{2}, \hspace{5mm} I^{2,\infty} = \frac{N - 2M + 4}{2}. \end{equation*}We require strings of length greater than one to have strictly finite rapidities. The maximal quantum number turns out to be given by
\begin{equation*} I^{j,\mbox{max}} = I^{j,\infty} - j. \end{equation*}We set \(M = N/2\), \(M_1 = M_1^< = N/2 - 2\) and \(M_2 = 1\). We thus obtain
\begin{equation*} I^{1,\infty} = \frac{N}{4} + \frac{1}{2}, \hspace{5mm} I^{2,\infty} = 2. \end{equation*}There is thus a single allowable quantum number for the two-string, \(I^{2}_1 = 0\). There are \(\frac{N}{2}\) available quantum number for finite rapidity one-strings, of which there are \(\frac{N}{2} - 2\), giving us \(\left( \begin{array}{c} N/2 \\ N/2 - 2 \end{array} \right) = \frac{N(N-2)}{8}\) states which are the \(S = 0, S^z = 0\) two-spinon states.
Here, we take \(M = N/2-1\), \(M_1 = M-2 = N/2-3 = M_1^<\), \(M_2 = 1\). The limiting quantum numbers are
\begin{equation*} I^{1,\infty} = \frac{N}{4} + 1, \hspace{5mm} I^{2,\infty} = 3 \end{equation*}so there are 3 slots for the two-string, and thus \(3\times \left( \begin{array}{c} N/2 + 1 \\ N/2 - 3 \end{array} \right) = (N + 2) N (N-2) (N-4)/128\) such states. These are the four-spinon states in this sector.
Here, we take \(M = N/2\), \(M_1^< = N/2-3\), \(M_1^\infty = 1\) and \(M_2 = 1\). The equations for the limiting quantum numbers then fall back onto the \(M \rightarrow M-1\) ones, so now \(I^{1,\infty} = \frac{N}{4} + 1\), \(I^{2\infty} = 3\). There are thus \(3\) available positions for the two-string, and \(\frac{N}{2} + 1\) available slots for the \(\frac{N}{2} - 3\) remaining finite rapidity one-strings. In total, there are thus \(3\times \left( \begin{array}{c} N/2 + 1 \\ N/2 - 3 \end{array} \right) = (N + 2) N (N-2) (N-4)/128\) such states. These are the four-spinon states in this sector.
Two two-strings
We take \(M = N/2\), \(M_1 = M_1^< = M-4 = N/2-4\), \(M_2 = 2\). The limiting quantum numbers are here
\begin{equation*} \pi (1 - \frac{M-5}{N} - \frac{4}{N}) = \frac{2\pi}{N} \frac{N-M+1}{2} = \frac{2\pi}{N} (\frac{N}{4} + \frac{1}{2}) \rightarrow I^{1,\infty} = \frac{N}{4} + \frac{1}{2}. \end{equation*} \begin{equation*} \pi (1 - 2 \frac{M-4}{N} - \frac{3}{N}) = \frac{2\pi}{N} \frac{N - 2M + 5}{2} \rightarrow I^{2,\infty} = \frac{5}{2} \end{equation*}There are thus 2 slots for 2 two-strings (1 possibility) and \(N/2\) slots for \(N/2 - 4\) one-strings, giving in total \(\frac{N (N-2) (N-4) (N-6)}{384}\) states, which are the \(S = 0\), \(S^z = 0\) four-spinon states.
One three-string
We take \(M = N/2\), \(M_1 = M_1^< = N/2-3\), \(M_3 = 1\). The limiting quantum numbers are
\begin{equation*} I^{1,\infty} = \frac{N}{4} + 1, \hspace{5mm} I^{3,\infty} = 3 \end{equation*}meaning that there is one available slot for the three-string, and \(N/2 +1\) slots for the \(N/2-3\) finite rapidity one-strings. This gives \((N + 2) N (N-2) (N-4)/384\) states, which are the four-spinon states in this \(S=0\), \(S^z=0\) sector.
Counting spinon states
Adding up the \(S=0\) and \(S=1\) two-spinon states, we obtain
\begin{equation*} \frac{N(N-2)}{8} + 3 \times \frac{N(N+2)}{8} = \frac{N(N+1)}{2} = \left( \begin{array}{c} N+1 \\ 2 \end{array} \right) \end{equation*}which is the correct total number of two-spinon states.
Adding the numbers of states in all the \(S=0, 1\) and \(2\) sectors gives (note: as expected, there are 2 \(S=0\) representations, 3 \(S=1\) ones, and one \(S=2\))
\begin{align*} \frac{N (N-2) (N-4) (N-6)}{384} + \frac{(N+2)N(N-2)(N-4)}{384} + 3\times \frac{(N+2) N (N-2) (N-4)}{128} + \nonumber \\ + 5\times \frac{(N+4)(N+2) N (N-2)}{384} = \left( \begin{array}{c} N+1 \\ 4 \end{array} \right) \hspace{5cm} \end{align*}which is the expected total number of four-spinon states.
Supplement: Completeness of the Bethe Ansatz for the \(M = 2\) case of the \(XXX\) antiferromagnet
If we specialize to \(M = 2\), we can solve the problem completely for arbitrary \(N\). Doing this illustrates peculiar features of the Bethe Ansatz which are swept under the rug by the string hypothesis, gives an idea of what is left behind, and justifies making the string approximation in most circumstances.
Let us begin from the Bethe equations
\begin{equation*} ~\mbox{atan}~ 2\lambda_1 - \frac{1}{N} ~\mbox{atan}~ (\lambda_1 - \lambda_2) = \pi \frac{I_1}{N}, \hspace{1cm} ~\mbox{atan}~ 2\lambda_2 + \frac{1}{N} ~\mbox{atan}~ (\lambda_1 - \lambda_2) = \pi \frac{I_2}{N} \end{equation*}Here, \(I_{1,2}\) are integers if \(N\) is odd, and half-odd integers if \(N\) is even.
Let us restrict to real \(\lambda_1 < \lambda_2\). For fixed \(\lambda_2\), taking \(\lambda_1\) to \(-\infty\) yields the lower limit
\begin{equation*} -\frac{\pi}{2} + \frac{\pi}{2N} = \pi \frac{I_1^{min}}{N}, \hspace{1cm} I^{min} = -\frac{N - 1}{2} \end{equation*}If \(\lambda_1 = -\infty\), the remaining Bethe equation becomes
\begin{equation*} ~\mbox{atan}~ 2\lambda_2 - \frac{\pi}{2N} = \pi \frac{I_2}{N}, \hspace{1cm} \lambda_2 = \frac{1}{2} \tan \frac{\pi}{2N}(2 I_2 + 1) \end{equation*}For \(I^{min} < I_2 < I^{max} = \frac{N-1}{2}\) this has a solution with finite \(\lambda_2\). Using that \(k_1 = 0\) and \(\phi = -\pi\) since \(\lambda_1 = -\infty\), the wavefunction then reads
<<h.l1mi>>
If we put \(\lambda_2 \rightarrow \infty\), we get \(k_2 = 0\) and \(\phi = \pi\). The Bethe equation for \(\lambda_1\) becomes
\begin{equation*} ~\mbox{atan}~ 2\lambda_1 + \frac{\pi}{2N} = \pi \frac{I_1}{N}, \hspace{1cm} \lambda_1 = \frac{1}{2} \tan \frac{\pi}{2N}(2 I_1 - 1) \end{equation*}with solution for finite real \(\lambda_1 < \lambda_2\) for \(I^{min} < I_1 < I^{max}\). The wavefunction then becomes
\begin{equation*} \Psi_2 (j_1, j_2) = e^{i k_1 j_1 - i\pi/2} - e^{i k_1 j_2 +i\pi/2} = -i (e^{i k_1 j_1} + e^{i k_1 j_2} ) \end{equation*}which coincides up to a constant with h.l1mi. In the particular limit \(\lambda_1 \rightarrow -\infty\), \(\lambda_2 \rightarrow \infty\), we get \(k_1 \rightarrow 0^-\), \(k_2 \rightarrow 0^+\), \(\phi \rightarrow -\pi\) so the Bethe wavefunction is a constant, which is not a solution of the (second part of the) eigenvalue equation.
All in all, we are thus able to construct
\begin{equation*} \left(\begin{array}{c} N-2 \\ 2 \end{array} \right) + N - 2 = \left(\begin{array}{c} N-1 \\ 2 \end{array} \right) \end{equation*}distinct Bethe wavefunctions with real rapidities in the interval \([-\infty, \infty]\). The first term is from counting wavefunctions with finite rapidities (for which \(I_1, I_2\) are chosen within the interval \(I^{min} < I < I^{max}\)), and the second term comes from wavefunctions with one infinite rapidity, obtained by choosing \(I_1 = I^{min}\) and \(I^{min} < I_2 < I^{max}\) or \(I^{min} < I_1 < I^{max}\) and \(I_2 = I^{max}\) (both choices generating the same set of wavefunctions).
There are thus
\begin{equation*} \left(\begin{array}{c} N \\ 2 \end{array} \right) - \left(\begin{array}{c} N-1 \\ 2 \end{array} \right) = N - 1 \end{equation*}wavefunctions which are not of Bethe form with real rapidities and distinct quantum numbers. This counting was done by Bethe himself in his original article 1931.Bethe.ZP.71.
To search for solutions off the real axis, we begin by noting that since the energy must be real, the two momenta \(k_{1,2} = u_{1,2} + i v_{1,2}\) must be such that
\begin{align*} 0 = \Im (\cos k_1 + \cos k_2) = \Im (\cos (u_1 + i v_1) + \cos (u_2 + i v_2)) \nonumber \\ = - (\sin u_1 \sinh v_1 + \sin u_2 \sinh v_2) \end{align*}Since the total momentum must also be real, we have
\begin{equation*} 0 = \Im (k_1 + k_2) = v_1 + v_2 \end{equation*}so \(\sinh v_1 = -\sinh v_2\) and therefore \(\sin u_1 = \sin u_2\), so \(u_2 = u_1\) or \(u_2 = \pi - u_1\). For the rapidities, with \(k_1 = u + i v\),
\begin{align*} 2\lambda_1 = \cot \frac{u + iv}{2} = \frac{\cos \frac{u+iv}{2}}{\sin \frac{u+iv}{2}} = \frac{ \cos \frac{u}{2} \cosh \frac{v}{2} - i \sin \frac{u}{2} \sinh \frac{v}{2}}{\sin \frac{u}{2} \cosh \frac{v}{2} + i \cos \frac{u}{2} \sinh \frac{v}{2}} \nonumber \\ = \frac{(\cos \frac{u}{2} \cosh \frac{v}{2} - i \sin \frac{u}{2} \sinh \frac{v}{2}) (\sin \frac{u}{2} \cosh \frac{v}{2} - i \cos \frac{u}{2} \sinh \frac{v}{2})} {\sin^2 \frac{u}{2} \cosh^2 \frac{v}{2} + \cos^2 \frac{u}{2} \sinh^2 \frac{v}{2}} \nonumber \\ = \frac{1/2}{1/4} \frac{\sin u - i \sinh v}{(1-\cos u)(\cosh v + 1) + (1 + \cos u)(\cosh v - 1)} \end{align*} \begin{equation*} 2\lambda_1 = \frac{\sin u - i \sinh v}{\cosh v - \cos u} \end{equation*}In the first case, we have \(k_2 = k_1^* = u - iv\) so
\begin{equation*} 2\lambda_2 = \frac{\sin u + i \sinh v}{\cosh v - \cos u} = 2\lambda_1^* \end{equation*}In the second case, we have \(k_2 = \pi - u - i v\) so
\begin{equation*} 2\lambda_2 = \frac{\sin u - i \sinh v}{\cosh v + \cos u} \end{equation*}⊂paragraph{First case: \(k_2 = k_1^* = u - iv\).} Put
\begin{equation*} \lambda_1 = \mu + i \nu = \lambda_2^* \end{equation*}The Bethe equations can be written
\begin{align*} \ln \frac{1 -2 \nu + 2 i \mu}{1 + 2\nu - 2i\mu} - \frac{1}{N} \ln \frac{1 - 2\nu}{1+2\nu} = 2\pi i \frac{I_1}{N}, \nonumber \\ \ln \frac{1 +2 \nu + 2 i \mu}{1 - 2\nu - 2i\mu} + \frac{1}{N} \ln \frac{1 - 2\nu}{1+2\nu} = 2\pi i \frac{I_2}{N}, \end{align*}Adding these gives
\begin{equation*} \ln \frac{1 + 2\nu + 2i\mu}{1 + 2\nu - 2i\mu} \frac{1 - 2\nu + 2i\mu}{1 - 2\nu - 2i\mu} = 2\pi i \frac{I_1 +I_2}{N} \end{equation*}whereas subtracting gives
\begin{equation*} \ln \frac{1 -2 \nu + 2 i \mu}{1 + 2\nu - 2i\mu} \frac{1 - 2\nu - 2i\mu}{1 +2 \nu + 2 i \mu} - \frac{2}{N} \ln \frac{1 - 2\nu}{1+2\nu} = 2\pi i \frac{I_1 - I_2}{N} \end{equation*}Equating the imaginary parts, we see that either \(I_1 = I_2\) and \(1-2\nu > 0\) or \(|I_1 - I_2| = 1\) and \(1-2\nu < 0\). Putting \(\nu = 1/2 - \delta\) with \(\delta < 1/2\),
\begin{equation*} \ln \frac{\delta + i \mu}{1 - \delta - i\mu} \frac{\delta - i\mu}{1 - \delta + i \mu} - \frac{2}{N} \ln \frac{\delta}{1 -\delta} = 2\pi i \frac{I_1 - I_2}{N} \end{equation*}so the equations become
<<h.be2>>
If \(\delta \rightarrow 0\), we must have \(\mu \rightarrow 0\). Asymptotically, we have \(\mu = \delta^{1/N}\) for \(\delta \rightarrow 0^+\). Then, \(\lambda_{1,2} \rightarrow \delta^{1/N} \pm i(1/2 - \delta)\) so \(\lambda_1 - \lambda_2 \rightarrow i (1-\delta)\). This means that \(\phi(\lambda_1 - \lambda_2) \rightarrow 2~\mbox{atan}~(i - i\delta) = \frac{1}{i} \ln \frac{\delta}{2} \rightarrow i\infty\). Also, \(\delta^{1/N} \pm i(1 - 2\delta) = \cot \frac{k_{1,2}}{2} = i \frac{e^{ik_{1,2}/2}+e^{-ik_{1,2}/2}} {e^{ik_{1,2}/2} - e^{-ik_{1,2}/2}}\). Taking \(k \rightarrow -i\infty\) we can write \(\frac{e^{ik/2}+e^{-ik/2}}{e^{ik/2} - e^{-ik/2}} = (1 + 2 e^{-ik} + ...)\) so we can take \(\Re{k_1} = \pi/2\). Similarly, we find that \(k_2 \rightarrow -i\infty + \pi/2\). The wavefunction becomes after a rescaling
\begin{equation*} \Psi_2 (j_1, j_2) = (-1)^{j_1} \delta_{j_1+1, j_2}. \end{equation*}This is a proper wavefunction for even \(N\) only. Another way of seeing this is to put \(\delta \rightarrow 0\) directly into h.be2, which becomes \(\pi = 2\pi \frac{I_1 + I_2}{N}\). Since \(I_1 + I_2\) must be integer, \(N\) must be even.
For \(\delta \neq 0\), the sign of \(\delta\) is fixed by \((-1)^{I_1 - I_2}\). Let's first look at \(\delta > 0\), so \(I_1 = I_2 \equiv I\). We call solutions with \(0 < \delta < 1/2\) ``narrow pairs''. This last equation can be solved for \(\mu\),
\begin{equation*} \left[\frac{\delta^2}{(1-\delta)^2}\right]^{1/N} = \frac{\mu^2 + \delta^2}{\mu^2 + (1-\delta)^2}, \hspace{1cm} \mu = \pm \left[ \frac{(1-\delta)^2 \left[\frac{\delta^2}{(1-\delta)^2}\right]^{1/N} - \delta^2}{1 - \left[\frac{\delta^2}{(1-\delta)^2}\right]^{1/N}} \right]^{1/2} \end{equation*}Note that the parametric curve \(\mu (\delta)\) is the same as \(\mu(1-\delta)\). This is fine, since from the definitions we really only need to consider \(\delta < 1/2\). Defining \(\xi = \frac{\delta}{1-\delta}\), \(\delta = \frac{\xi}{1+\xi}\), \(1-\delta = \frac{1}{1+\xi}\), we get (\(\mu > 0\) if \(I > 0\), with similar equations holding for \(\mu < 0\), which we must choose for \(I < 0\))
\begin{equation*} \mu = \frac{1}{1+\xi} \left[ \frac{\xi^{2/N} - \xi^2}{1 - \xi^{2/N}} \right]^{1/2} \end{equation*}Then,
\begin{equation*} \frac{\mu}{1-\delta} = \left[ \frac{\xi^{2/N} - \xi^2}{1 - \xi^{2/N}} \right]^{1/2}, \hspace{1cm} \frac{\mu}{\delta} = \frac{1}{\xi} \left[ \frac{\xi^{2/N} - \xi^2}{1 - \xi^{2/N}} \right]^{1/2}. \end{equation*}The Bethe equations are solved if
<<h.np>>
The left-hand side is a monotonously increasing function of \(\xi\) for \(0 < \xi < 1\). For \(\xi = 0\), the value is \(\pi/2\). The maximum occurs at \(\xi = 1\). There, we have \(\mu = \frac{\sqrt{N-1}}{2}\) and \(\delta = 1/2\), meaning that we are returning to the real axis. Since
\begin{equation*} \lim_{\xi \rightarrow 1} \frac{\xi^{2/N} - \xi^2}{1 - \xi^{2/N}} = \frac{2/N - 2}{-2/N} = N-1 = \lim_{\xi \rightarrow 1} \frac{1}{\xi} \frac{\xi^{2/N} - \xi^2}{1 - \xi^{2/N}} \end{equation*}we have that the max is equal to \(2 ~\mbox{atan}~ \sqrt{N-1}\). The \(I\) we can choose can be written as \(\frac{N-1}{2} - n\), \(n = 0, 1, ...\) so we lose the first (pair of, since this also holds for \(I < 0\), so \(\mu < 0\)) complex solutions for \(N > N_c\) where
\begin{equation*} 2 ~\mbox{atan}~ \sqrt{N_c - 1} = \pi (1-3/N_c), \hspace{1cm} N_c = 21.8649. \end{equation*}(this is the equation for \(n = 1\); the one for \(n = 0\) has no solution, so we never lose it). The number \(n_{ex} (N)\) of excluded narrow pairs for given size \(N\) is given by \(2\lfloor n\rfloor\), where \(n\) is solution to
<<h.nex>>
Therefore,
\begin{equation*} n_{ex} = \lfloor \frac{N - 1}{2} - \frac{N}{\pi} ~\mbox{atan}~ \sqrt{N-1} \rfloor \end{equation*}The critial values of \(N\) are thus \(N_{c2} = 21.8649\), \(N_{c4} = 61.3488\), \(N_{c6} = 120.568\), \(N_{c8} = 199.525\), \(N_{c10} = 246.406\), \(N_{c12} = 298.222\), etc. For large \(N\), we have that
\begin{align*} n_{ex} = \lfloor \frac{N-1}{2} - \frac{N}{2\pi i} \ln \frac{1 + i \sqrt{N-1}}{1-i\sqrt{N-1}} \rfloor = \lfloor -\frac{1}{2} - \frac{N}{2\pi i} \ln \frac{1 - i/\sqrt{N-1}}{1+i/\sqrt{N-1}} \rfloor \nonumber \\ = \lfloor -\frac{1}{2} - \frac{N}{\pi} (- (N-1)^{-1/2} + \frac{1}{3} (N-1)^{-3/2} + O(N^{-5/2}) \rfloor \nonumber \\ = \lfloor -\frac{1}{2} + \frac{\sqrt{N}}{\pi} ( (1-1/N)^{-1/2} - \frac{1}{3} N^{-1} + O(N^{-2}) \rfloor \nonumber \\ = \lfloor -\frac{1}{2} + \frac{\sqrt{N}}{\pi} (1 + \frac{1}{6} N^{-1} + O(N^{-2}) \rfloor = \lfloor \frac{\sqrt{N}}{\pi} - \frac{1}{2} + \frac{N^{-1/2}}{6\pi} + O (N^{-3/2}) \rfloor \end{align*}This agrees with the result in reference 1992.Essler.JPA.25, where \(n_{max} - 1 = n_{ex}\) defined here.
For \(I_1 = I_2\), the number of choices of \(I\) at our disposal is fixed by observing that equation h.np can only be solved for \(\xi > 0\) if \(\pi/2 < 2\pi \frac{I}{N} < \pi\), so \(\frac{N}{4} < \frac{N-1}{2} - n < \frac{N}{2}\), \(\frac{N-2}{4} > n > 1/2\), and therefore \(n = 1, ..., \lfloor \frac{N-3}{4} \rfloor\). We thus have \(2⌊ \frac{N-3}{4} ⌋
- 2nex(N)\) narrow pair solutions.
Similarly, for the case \(\delta < 0\) (which we call ``wide pairs''), where \(|I_1 - I_2| = 1\), we get (writing \(\delta = -\tilde{\delta}\))
\begin{equation*} 2 ~\mbox{atan}~ \frac{\mu}{1+\tilde{\delta}} - 2~\mbox{atan}~ \frac{\mu}{\tilde{\delta}} = 2\pi \frac{I_1 + I_2}{N} \end{equation*} \begin{equation*} \frac{\tilde{\delta}}{1+\tilde{\delta}} = \left[ \frac{\mu^2 + {\tilde{\delta}}^2}{\mu^2 + (1+\tilde{\delta})^2} \right]^{N/2} \end{equation*}Solving for \(\mu\),
\begin{equation*} \mu = \pm \left[ \frac{(1+\tilde{\delta})^2 \left[\frac{{\tilde{\delta}}^2}{(1+\tilde{\delta})^2}\right]^{1/N} - {\tilde{\delta}}^2}{1 - \left[\frac{{\tilde{\delta}}^2}{(1+\tilde{\delta})^2}\right]^{1/N}} \right]^{1/2} \end{equation*}Defining \(\tilde{\xi} = \frac{\tilde{\delta}}{1 + \tilde{\delta}}\), so \(\tilde{\delta} = \frac{\tilde{\xi}}{1-\tilde{\xi}}\) and \(1 + \tilde{\delta} = \frac{1}{1-\tilde{\xi}}\). Since we assume \(0 < \tilde{\delta} < \infty\), we have \(0 < \tilde{\xi} < 1\). If \(I_1 + I_2 > 0\), we must choose \(\mu < 0\),
\begin{equation*} \mu = -\frac{1}{1-\tilde{\xi}} \left[ \frac{{\tilde{\xi}}^{2/N} - {\tilde{\xi}}^2}{1 - {\tilde{\xi}}^{2/N}} \right]^{1/2} \end{equation*}Then,
\begin{equation*} \frac{\mu}{1+\tilde{\delta}} = -\left[ \frac{{\tilde{\xi}}^{2/N} - {\tilde{\xi}}^2}{1 - {\tilde{\xi}}^{2/N}} \right]^{1/2}, \hspace{1cm} \frac{\mu}{\tilde{\delta}} = -\frac{1}{\tilde{\xi}} \left[ \frac{{\tilde{\xi}}^{2/N} - {\tilde{\xi}}^2}{1 - {\tilde{\xi}}^{2/N}} \right]^{1/2}. \end{equation*}The Bethe equations are solved if
\begin{equation*} -~\mbox{atan}~ \left[ \frac{{\tilde{\xi}}^{2/N} - {\tilde{\xi}}^2}{1 - {\tilde{\xi}}^{2/N}} \right]^{1/2} + ~\mbox{atan}~ \frac{1}{\tilde{\xi}} \left[ \frac{{\tilde{\xi}}^{2/N} - {\tilde{\xi}}^2}{1 - {\tilde{\xi}}^{2/N}} \right]^{1/2} = \pi \frac{I_1 + I_2}{N} \end{equation*}For the allowed values of \(\tilde{\xi}\), the left-hand side takes on all values in the interval \(]0, \pi/2[\), so \(0 < I_1 + I_2 < N/2\). But \(I_1 + I_2\) can here be written as \(N - 2n\) with \(n \geq 0\), so we have \(N/2 > n > N/4\) so \(\lfloor \frac{N+1}{4}\rfloor \leq n \leq \lfloor \frac{N-1}{2} \rfloor\). There are thus \(\lfloor \frac{N-1}{2} \rfloor - \lfloor \frac{N+1}{4} \rfloor + 1\) choices for \(n > 0\). (Note: this is equal to \(\lfloor \frac{N-1}{4} + 1\rfloor\)). We can thus construct \(2 \lfloor \frac{N-1}{2} \rfloor - 2\lfloor \frac{N+1}{4} \rfloor + 2\) distinct wide pair Bethe states.
The total number of states that we have constructed is thus
\begin{align*} 1 - (N \% 2) + 2 \lfloor \frac{N-3}{4}\rfloor - n_{ex}(N) + 2 \lfloor \frac{N-1}{2} \rfloor - 2\lfloor \frac{N+1}{4} \rfloor + 2 \nonumber \\ = (1 - (N \% 2) + 2 \lfloor \frac{N-1}{2}) + (2 \lfloor \frac{N-3}{4}\rfloor - 2\lfloor \frac{N+1}{4} \rfloor + 2) - n_{ex}(N) \nonumber \\ = N - 1 + 0 - n_{ex}(N) = N - 1 - n_{ex}(N) \end{align*}⊂paragraph{Second case: \(k_2 = \pi - k_1 = \pi - u - iv\), \(v \neq 0\).} We have then
\begin{equation*} 2\lambda_2 = \cot \frac{\pi - k_1}{2} = \tan \frac{k_1}{2} = \frac{1}{2\lambda_1} \end{equation*}The Bethe equations become
\begin{equation*} ~\mbox{atan}~ 2\lambda_1 - \frac{1}{N} ~\mbox{atan}~ \frac{\lambda_1^2 - 1/4}{\lambda_1} = \pi \frac{I_1}{N}, \hspace{0.3cm} ~\mbox{atan}~ \frac{1}{2\lambda_1} + \frac{1}{N} ~\mbox{atan}~ \frac{\lambda_1^2 - 1/4}{\lambda_1} = \pi \frac{I_2}{N} \end{equation*}Adding these, we get (\(\lambda \equiv \lambda_1\))
\begin{align*} ~\mbox{atan}~ 2\lambda + ~\mbox{atan}~ \frac{1}{2\lambda} = \frac{1}{2i} \ln \frac{1 + 2i\lambda}{1-2i\lambda} \frac{1 + i/2\lambda}{1-i/2\lambda} = \pi/2 ~~\mbox{mod} ~~\pi = \pi \frac{I_1 + I_2}{N}, \nonumber \\ I_1 + I_2 = N/2 ~~ \mbox{mod} ~N \end{align*}Subtracting,
\begin{equation*} ~\mbox{atan}~ 2\lambda - ~\mbox{atan}~ \frac{1}{2\lambda} - \frac{2}{N} ~\mbox{atan}~ \frac{\lambda^2 - 1/4}{\lambda} = \pi\frac{I_1 - I_2}{N} \end{equation*}The left-hand side simplifies by using
\begin{equation*} ~\mbox{atan}~ 2\lambda - ~\mbox{atan}~ \frac{1}{2\lambda} = \frac{1}{2i} \ln \frac{1 + 2i\lambda}{1-2i\lambda} \frac{1 - i/2\lambda}{1+i/2\lambda} %=\frac{1}{2i} \ln \frac{1 + i \frac{\lambda^2 - 1/4}{\lambda}}{1 - i \frac{\lambda^2 - 1/4}{\lambda}} = ~\mbox{atan}~ \frac{\lambda^2 - 1/4}{\lambda} \end{equation*}so
\begin{align*} ~\mbox{atan}~ \frac{\lambda^2 - 1/4}{\lambda} = \pi \frac{I_1 - I_2}{N-2}, \hspace{1cm} \frac{\lambda^2 - 1/4}{\lambda} = \tan \pi \frac{I_1 - I_2}{N-2} \equiv f, \nonumber \\ \lambda = \frac{f \pm \sqrt{f^2 + 1}}{2} \end{align*}Since \(f\) is real, we always have that \(\lambda\) is real, so \(v = 0\), which contradicts our hypothesis (since both rapidities here are real, these wavefunctions have already been counted in the previous section).
⊂paragraph{Coinciding quantum numbers} If we put \(I_1 = I_2 \equiv I\), we get
\begin{equation*} ~\mbox{atan}~ 2\lambda_1 - \frac{1}{N} ~\mbox{atan}~ (\lambda_1 - \lambda_2) = \pi \frac{I}{N} = ~\mbox{atan}~ 2\lambda_2 + \frac{1}{N} ~\mbox{atan}~ (\lambda_1 - \lambda_2) \end{equation*}so
\begin{equation*} ~\mbox{atan}~ 2\lambda_1 + ~\mbox{atan}~ 2\lambda_2 = 2\pi \frac{I}{N}, \hspace{1cm} ~\mbox{atan}~ 2\lambda_1 - ~\mbox{atan}~ 2\lambda_2 = \frac{2}{N} ~\mbox{atan}~ (\lambda_1 - \lambda_2) \end{equation*}The second equation can be rewritten (using \(\lambda_1 \equiv \lambda\) and \(\lambda_2 \equiv \lambda + \delta\))
\begin{align*} 2\lambda = \tan \left( ~\mbox{atan}~ (2\lambda +2\delta) - \frac{2}{N} ~\mbox{atan}~ \delta \right) \nonumber \\ = \tan \left( \frac{\pi}{2} - ~\mbox{atan}~ \frac{1}{2\lambda +2\delta} - \frac{2}{N} ~\mbox{atan}~ \delta \right) \nonumber \\ = \frac{1}{\tan \left(~\mbox{atan}~ \frac{1}{2\lambda +2\delta} + \frac{2}{N} ~\mbox{atan}~ \delta \right)} = \frac{1 - \frac{1}{2\lambda + 2\delta} \tan(\frac{2}{N}~\mbox{atan}~\delta)}{\tan(\frac{2}{N}~\mbox{atan}~\delta) + \frac{1}{2\lambda + 2\delta}} \end{align*}so, defining \(t = \tan (\frac{2}{N} ~\mbox{atan}~ \delta)\),
\begin{equation*} 2\lambda (t (2\lambda + 2\delta) + 1) = 2\lambda + 2\delta -t, \hspace{0.3cm} \lambda^2 + \lambda \delta + \frac{1}{4} - \frac{\delta}{2t} = 0, \hspace{0.3cm} 2\lambda = -\delta + \sqrt{\delta^2 + \frac{2\delta}{t} - 1} \end{equation*}Therefore, \(2\lambda_1 = g - \delta\) and \(2\lambda_2 = g + \delta\), with \(g = \sqrt{\delta^2 + \frac{2\delta}{t} - 1}\). The first Bethe equation gives
\begin{equation*} ~\mbox{atan}~(g - \delta) + ~\mbox{atan}~(g + \delta) = 2\pi \frac{I}{N} \end{equation*}The left-hand side takes its minimum value at \(\delta = 0\). Then, \(\lim_{\delta \rightarrow 0} \frac{t}{\delta} = \frac{2}{N}\). We thus find, writing \(I = \frac{N-1}{2} - n\),
\begin{equation*} 2 ~\mbox{atan}~ \sqrt{N-1} = \frac{\pi}{N} (N - 1 - 2n) \end{equation*}which is the same condition as h.nex. Therefore, each time we lose a narrow pair, we gain an extra real solution obtained from using the same quantum numbers for the two rapidities.
The total number of solutions we have found is thus
\begin{equation*} \left(\begin{array}{c} N \\ 2 \end{array} \right) \end{equation*}which coincides with the dimension of the Hilbert subspace. There are \(\left(\begin{array}{c} N - 2 \\ 2 \end{array} \right)\) wavefunctions with real, finite rapidities with distinct quantum numbers, \(N-2\) wavefunctions with one infinite rapidity, one wavefunction with \(\lambda_{1,2} = \pm i/2\) for \(N\) even, \(2\lfloor \frac{N-3}{4} \rfloor - n_{ex}(N)\) narrow pair eigenstates, \(2\lfloor \frac{N-1}{2} \rfloor - 2\lfloor \frac{N+1}{4} \rfloor + 2\) wide pair eigenstates and \(n_{ex}(N)\) extra real pairs with coinciding quantum numbers. The two-particle sector of the isotropic model is thus fully understood.
Exercise: extend this to arbitrary \(M \leq N/2\) (email me if you manage). Some steps in this direction are taken in 2007.Hagemans.JPA.40.
Further spin chains
The axial Heisenberg antiferromagnet (XXZ with \(\Delta > 1\))
Let us specialize our equations to the case of the gapped antiferromagnet with anisotropy \(\Delta > 1\). We make use of parameter \(\eta\) such that \(\Delta = \cosh \eta\). We will adopt the convention that \(\eta > 0\).
We introduce rapidities \(\lambda\) defined in the physical strip
\begin{equation*} -\frac{\pi}{2} < \Re \lambda \leq \frac{\pi}{2}, \hspace{10mm} |\Im \lambda| < \infty \end{equation*}and parametrize the bare momenta in terms of these as
<<a.l>>
and thus
\begin{equation*} k (\lambda) = \frac{1}{i} \ln \frac{\sin (\lambda + i\eta/2)}{\sin (\lambda - i\eta/2)} = \pi - 2 ~\mbox{atan}~ \frac{\tan \lambda}{\tanh \frac{\eta}{2}}. \end{equation*}The Bethe equations in this regime take the form
<<a.be>>
<<a.bel>>
where the kernel is now
<<a.phin>>
The integer part of the kernel (second term) guarantees monotonicity for real \(\lambda\). This is important for the classification of states (you can find a partial discussion in 2008.Caux.JSTAT.P08006).
The energy of a state in an external magnetic field \(h\) is given as a function of the rapidities by
<<a.e>>
whereas the momentum, which is the sum over quasi-momenta associated to each rapidity, has a simple representation in terms of the quantum numbers:
<<a.p>>
In the presence of strings, the same construction applies as for \(XXX\). The Bethe equations again get reduced to a Bethe-Gaudin-Takahashi form, and the string-string scattering phase shift is still given by the form h.phijk.
The planar Heisenberg chain (XXZ with \(-1 < \Delta < 1\))
Let us now turn to the anisotropic antiferromagnet in the gapless regime \(0 < \Delta < 1\). The anisotropy is parametrized by \(\zeta = \mbox{acos} \Delta\) with \(\zeta \in ]0, \pi/2[\). The bare momenta are here parametrized in terms of rapidities as
<<p.l>>
again such that \(k(\lambda = 0) = \pi\). Using this parametrization, the scattering phase shift again becomes function of the rapidity difference only. The Bethe equations xxz.be then become
<<p.be>>
Taking logs and defining the fundamental kernel
<<p.phin>>
the Bethe equations are rewritten as
<<p.bel>>
which are precisely of the same form as h.bel, the only difference being the definition of the \(\phi_n\) kernels. The energy of a state described by the set of rapidities \(\{ \lambda_a \}\) is then
<<p.e>>
whereas the momentum again has a simple representation in terms of the quantum numbers,
<<p.p>>
String state classification
Following Takahashi and Suzuki 1972.Takahashi.PTP.48, we take \(\zeta/\pi\) to be a real number between \(0\) and \(1\), which is expressed as a continued fraction of real positive integers as
\begin{equation*} \frac{\zeta}{\pi} = \frac{1|}{|\nu_1} + \frac{1|}{|\nu_2} + ... \frac{1|}{|\nu_l}, \hspace{1cm} \nu_1, ..., \nu_{l-1} \geq 1, \nu_l \geq 2. \end{equation*}For large \(N\), rapidities congregate to form strings centered either on the real line (for positive parity strings) or on the axis \(i\pi/2\) (for negative parity strings),
<<p.sh>>
where the allowable lengths \(n_j\) and parities \(v_j = \pm 1\) are to be determined. In a string configuration, the parameters \(\delta^{n_j, a}_{\alpha}\) are exponentially suppressed with system size.
The classification of allowable string types in the thermodynamic limit proceeds according to the following algorithm. First, the positive integer series \(y_{-1}, y_0, y_1, \ldots, y_l\) and \(m_0, m_1, \ldots, m_l\) are defined as
\begin{align*} &y_{-1} = 0, ~~y_0 = 1, ~~y_1 = \nu_1, ~~\mbox{and}~~ y_i = y_{i-2} + \nu_i y_{i-1}, ~~i = 2, \ldots, l, \nonumber \\ &m_0 = 0, ~~m_i = \sum_{k = 1}^i \nu_k. \end{align*}Lengths and parities are then given by (our conventions here have the advantage of giving a proper ordering of string lengths, \(n_j > n_k\), \(j > k\))
\begin{equation*} n_j = y_{i-1} + (j - m_i)y_i, ~~v_j = (-1)^{\lfloor (n_j - 1)\zeta/\pi \rfloor}, \hspace{1cm} m_i \leq j < m_{i+1}. \end{equation*}The total number of possible strings is \(N_s = m_l + 1\), and the index \(j\) runs over the set \(1, ..., N_s\). The real parameters \(\lambda_{\alpha}^{n_j}\) represent the centers of strings with length \(n_j\) and parity \(v_j\), and are hereafter noted as \(\lambda^j_{\alpha}\), \(\alpha = 1, ..., M_j\), where \(M_j\) is the number of strings of length \(n_j\) in the eigenstate under consideration. We therefore have the constraint \(\sum_{j = 1}^{N_s} n_j M_j = M\).
In a string configuration, many factors appearing in the Bethe equations become of the indeterminate form \(\delta/\delta\). Remultiplying p.be for each member of a particular string gets rid of these factors, and allows one to rewrite the whole set of Bethe equations in terms of a reduced set involving only the string centers \(\lambda_{\alpha}^j\). Doing this, one finds (for \(N\) even) the reduced set of Bethe-Takahashi equations 1972.Takahashi.PTP.48
<<p.bgt>>
where
<<p.ej>>
and
<<p.ejk>>
For the state classification and computation, it is preferable to work with the logarithmic form
<<p.bgtl>>
where \(I^j_{\alpha}\) is integer if \(M_j\) is odd, and half-integer if \(M_j\) is even. The dispersion kernels and scattering phases appearing here are
\begin{align*} \phi_j (\lambda) &= 2 v_j ~\mbox{atan} \left[(\tan n_j\zeta/2)^{-v_j}\tanh \lambda \right], \nonumber \\ \Phi_{jk}(\lambda) &= (1-\delta_{n_j n_k}) \phi_{|n_j-n_k|}(\lambda) + 2\phi_{|n_j-n_k|+2}(\lambda) + \ldots + 2\phi_{n_j+n_k-2} (\lambda) + \phi_{n_j+n_k} (\lambda). \end{align*}The energy and momentum of a string are given by
<<p.eps>>
so the total momentum is again expressible in terms of the string quantum numbers as
<<p.p>>
in which \(T_{v=+}\) is the total number of excitations with positive parity.
Further continuum models
The attractive Lieb-Liniger gas
In the repulsive case, given a proper set of quantum numbers \(\{ I \}\), the solution of the Bethe equations for the set of rapidities \(\{ \lambda \}\) exists and is unique 1969.Yang.JMP.10 due to the convexity of the Yang-Yang action. Furthermore all these solutions have real rapidities \(\lambda_i\). For the attractive case, the situation is completely different. We will define \(\bar{c}=-c > 0\) as the interaction parameter; let us rewrite our Bethe equations as
<<al.be>>
Consider now a complex rapidity \(\lambda_{\alpha} = \lambda + i \eta\). The Bethe equation for this rapidity is
\begin{equation*} e^{i\lambda_{\alpha} L} = e^{i \lambda L - \eta L} = \prod_{\beta \neq \alpha} \frac{\lambda_{\alpha} - \lambda_{\beta} - i\bar{c}} {\lambda_{\alpha} - \lambda_{\beta} + i\bar{c}}. \end{equation*}We consider finite \(N\) and \(L \rightarrow \infty\). If \(\eta > 0\), we have \(e^{-\eta L} \rightarrow 0\) on the left-hand side. Looking at the finite product on the right-hand side, we conclude that there must thus be a rapidity \(\lambda_{\alpha'}\) such that \(\lambda_{\alpha'} = \lambda_{\alpha} - i \bar{c} + \mbox{O}(e^{-\eta L})\). On the other hand, if \(\eta < 0\), we have \(e^{-\eta L} \rightarrow \infty\) on the left-hand side, and there must thus be a rapidity \(\lambda_{\alpha'}\) such that \(\lambda_{\alpha'} = \lambda_{\alpha} + i \bar{c} + \mbox{O}(e^{-|\eta| L})\). The rapidities thus like to arrange themselves into clusters, the elements of each cluster being evenly-spaced by \(\bar{c}\) in the imaginary direction. Such clusters represent bound states of particles, and we will call them strings.
For a given number of atoms \(N\), we can construct eigenstates with fixed string content by partitioning \(N\) into \(N_j\) strings of length \(j\), denoting the total number of strings as \(N_s\). We clearly have
\begin{equation*} N = \sum_{j} j N_j, \hspace{1cm} N_s = \sum_{j} N_j. \end{equation*}Specifically, we will parametrize the string rapidities as
<<al.sh>>
with exponentially small deviations \(\delta \sim e^{-(cst)L}\) provided \(N_s/L \rightarrow 0\). In our string notation, the index \(a = 1, \dots, j\) labels rapidities within the string, and \(\alpha = 1, \dots, N_j\) labels strings of a given length.
We stress that perfect strings (i.e. with all the \(\delta_i=0\)) are exact eigenstates in the limit \(L\to\infty\) with \(N_s/L \rightarrow 0\) for arbitrary \(N\). It is then natural to consider the limit \(L\to\infty\) at fixed \(N\). This is different from what done in the repulsive case where the limit \(N,L\to\infty\) at fixed density \(N/L\) is performed. Here, the \(N\) particles remain strongly correlated and bound to one another even when \(L \to \infty\).
These bound states should be viewed as individual particles of mass \(j\), with momentum and energy of the string centered on \(\lambda^j_{\alpha}\) given by
<<al.eps>>
Such strings are known but not commonly discussed in the literature on the Bose gas, since they do not appear in the repulsive case. However, their direct equivalents exist in integrable spin chains, where they have been extensively studied. The technology to treat them, at least on the level of eigenstates, is thus completely standard.
Bethe equations for strings
The Bethe equation al.be in terms of the string rapidities al.sh are
\begin{align*} e^{i \lambda^{j,a}_{\alpha} L} &= \prod_{(k, \beta, b) \neq (j, \alpha, a)} \frac{\lambda^{j, a}_{\alpha} - \lambda^{k, b}_{\beta} - i\bar{c}}{\lambda^{j, a}_{\alpha} - \lambda^{k, b}_{\beta} + i\bar{c}} \nonumber \\ &= \prod_{(k, \beta) \neq (j, \alpha)} \prod_{b=1}^k \frac{\lambda^j_{\alpha} - \lambda^k_{\beta} + i\bar{c} (\frac{j-k}{2} - a + b - 1)} {\lambda^j_{\alpha} - \lambda^k_{\beta} + i\bar{c} (\frac{j-k}{2} - a + b + 1)} \prod_{b \neq a} \frac{\bar{c} (-a + b - 1) + \delta^{j, (a,b)}_{\alpha}}{\bar{c} (-a + b + 1) + \delta^{j, (a,b)}_{\alpha}} \hspace{10mm} \end{align*}where we have separated inter- and intra-string parts, dropped all string deviations for inter-string factors, and denoted \(\delta^{j, a}_{\alpha} - \delta^{j, b}_{\alpha} = \delta^{j, (a,b)}_{\alpha}\) in the intra-string part. Simplified Bethe equations are obtained by taking the product of these equations within the string considered. The left-hand side becomes
\begin{equation*} \prod_{a=1}^j e^{i \lambda^{j,a}_{\alpha} L} = e^{i j\lambda^j_{\alpha} L}. \end{equation*}On the right-hand side, we have
\begin{equation*} \prod_{a=1}^j \prod_{b \neq a} \frac{\bar{c} (-a + b - 1) + \delta^{j, (a,b)}_{\alpha}}{\bar{c} (-a + b + 1) + \delta^{j, (a,b)}_{\alpha}} = (-1)^{j(j+1)} = 1 \end{equation*}for the intra-string part, and (writing \(\lambda = \lambda^j_{\alpha} - \lambda^k_{\beta}\))
\begin{equation*} \prod_{a=1}^j \prod_{b=1}^k \frac{\lambda + i\bar{c} (\frac{j-k}{2} - a + b - 1)} {\lambda + i\bar{c} (\frac{j-k}{2} - a + b + 1)} = e_{|j - k|} (\lambda) e_{|j-k| + 2}^2 (\lambda) e_{|j - k| + 4}^2 (\lambda) ... e_{j+k - 2}^2 (\lambda) e_{j+k} (\lambda) \equiv E_{jk} (\lambda) \end{equation*}where
\begin{equation*} e_j (\lambda) = \frac{\lambda - i\bar{c}j/2}{\lambda + i\bar{c}j/2}. \end{equation*}The exponential form of the Bethe equations has thus been reduced to the set of \(N_s\) coupled equations for the string centers \(\lambda^j_{\alpha}\),
\begin{equation*} e^{i j \lambda^j_{\alpha}L} = \prod_{(k, \beta) \neq (j, \alpha)} E_{jk} (\lambda^j_{\alpha} - \lambda^k_{\beta}). \end{equation*}Taking the logarithm and defining
\begin{equation*} \phi_j (\lambda) = 2 ~\mbox{atan}~ \frac{2\lambda}{\bar{c} j} \end{equation*}such that \(-i \log (-e_j (\lambda)) = \phi_j(\lambda)\), we find the reduced Bethe equations
<<al.bel>>
with \(I_{\alpha}^j\) half-odd integer (integer) if \(N_j\) is even (odd), and where the scattering phase shifts are
<<al.phijk>>
These strings are stable particles under scattering with one another, and are therefore soliton-like objects. One point worth emphasizing is that the scattering phase shifts al.phijk are simply those of breathers in the classical limit \(\beta \rightarrow 0\) of the sine-Gordon model after a trivial reparametrization of the rapidity. The sine-Gordon soliton's mass is in this limit much higher than that of the breathers, which have an evenly-spaced rest mass.
The ground state
The lowest energy state will be obtained by forming a bound state of all \(N\) particles centered on zero 1964.McGuire.JMP.5, namely by choosing
\begin{equation*} \lambda^{N,a} = i \frac{\bar{c}}{2} (N+1 - 2a) + \mbox{O}(\delta)\,. \end{equation*}The corresponding energy is
<<al.e0>>
Note that this goes like \(N^3\), unlike the repulsive case where the energy is not extensive. Although our results are not limited to this case, we will often consider the limit of a large number of particles \(N \gg 1\), with weak interactions \(\bar{c}\) such that the parameter \(g = \bar{c} N\) remains finite. In this case, the ground state energy per particle also remains finite, \(E_{GS} = -{g^2}/{12}\). We will find some similarly simplified limiting values for the correlations functions. It is however important to note that this is not a conventional thermodynamic limit with finite energy density as in the repulsive case.
Excited states
Excitations above the ground state are then obtained by either simply giving momentum to the ground state \(N\) string, or more elaborately by partitioning it into smaller strings to which individual momenta can be given. We consider here only the \(N\) atom sector relevant for the dynamical structure factor. The case of states with \(N-1\) (or less) atoms trivially follows.
We will label the string content of eigenstates by column-separated entries specifying the length and number of each different string type. For example \(N-M:M\) will be a state with a \(N-M\) string and a \(M\) string, and \(N-M_1-2M_2:M_1:(M_2)_2\) a state with an \(N - M_1 - 2M_2\) string, an \(M_1\) string and two \(M_2\) strings.
Single-particle states
Single-particle excited states will be obtained by giving finite momentum to the ground state \(N\)-string,
\begin{equation*} \mu^{N,a} = \mu + i \frac{\bar{c}}{2} (N+1 - 2a) + \mbox{O}(\delta). \end{equation*}Such states have energy above the ground state given by
\begin{equation*} \omega_{N} (\mu) \equiv E_\mu-E_{GS}=N \mu^2 = k_{\mu}^2/N \end{equation*}where \(k_{\mu} = N \mu\) is the total state momentum. For these states, there is only one Bethe equation for the string center \(\mu\), namely \(\mu = 2\pi {I}/{NL}\) with \(I\) an integer, so that the momentum is quantized as for a free wave, \(k_{\mu} = 2\pi {I}/{L}\). In the limit of large \(N\), this energy band becomes flat and quasi-degenerate with the ground state.
Two-particle states
These are obtained by splitting up the ground-state \(N\) string in two pieces. In general, consider having an \(N-M\) and an \(M\) string:
\begin{align*} \mu^{N-M,a} &= \mu_s + i \frac{\bar{c}}{2} (N - M +1 - 2a) + \mbox{O}(\delta), \hspace{1cm} a = 1, ..., N-M, \nonumber \\ \mu^{M,a} &= \mu_M + i \frac{\bar{c}}{2} (M + 1 - 2a) + \mbox{O}(\delta), \hspace{1cm} a = 1, ..., M. \end{align*}The energy of this state above the ground state is given by
\begin{equation*} \omega_{N-M:M} (\mu_s, \mu_M) = \omega^0_{N-M:M} + (N-M) \mu_s^2 + M \mu_M^2, \end{equation*}where we have defined the rest energy
\begin{equation*} \omega^0_{N-M:M} = \frac{\bar{c}^2}{4} N M (N-M). \end{equation*}The total momentum is the sum of the two string momenta,
\begin{equation*} k = k_s + k_M = (N-M) \mu_s + M \mu_M, \end{equation*}so we can write the energy as
\begin{equation*} \omega_{N-M:M} (k_s, k_M) = \omega^0_{N-M:M} + \frac{k_s^2}{N-M} + \frac{k_M^2}{M}. \end{equation*}Similarly to the single-particle case, the Bethe equations are here very simple, namely
\begin{align*} (N-M) \mu_s L - \Phi_{N-M,M} (\mu_s - \mu_M) &= 2\pi I_s, \nonumber \\ M \mu_M L + \Phi_{N-M,M} (\mu_s - \mu_M) &= 2\pi I_M, \end{align*}with \(I_s, I_M\) integers. In the limit of large L, we can thus ignore the scattering phase shift, and take \(\mu_s\) and \(\mu_M\) as free parameters. The total momentum \(k\) of the state can take on any value \(2\pi I/L\), but the energy is bounded from below by
\begin{equation*} \omega^l_{N-M:M} (k) = \omega^0_{N-M:M} + \frac{k^2}{N}. \end{equation*}Given external frequency \(\omega\) and momentum \(k\) parameters, there are two solutions to the dynamical constraints, namely
\begin{align*} \mu_s^{\pm}(k,\omega) &= \frac{k}{N} \mp \left[\frac{M}{N(N-M)}\right]^{1/2} [\omega - \omega^l_{N-M:M}(k)]^{1/2}, \nonumber \\ \mu_M^{\pm}(k,\omega) &= \frac{k}{N} \pm \left[\frac{N-M}{NM}\right]^{1/2} [\omega - \omega^l_{N-M:M}(k)]^{1/2}. \end{align*}Therefore, in the large \(L\) limit, these states for a two-fold degenerate continuum beginning at the lower threshold \(\omega^l_{N-M:M} (k)\) and extending to arbitrarily high energy,
\begin{equation*} \mbox{N-M:M continuum:} \hspace{1cm} \omega^l_{N-M:M}(k) \leq \omega < \infty. \label{eq:1DBG:N-M:Mcontinuum} \end{equation*}For finite \(L\), this is of course not strictly a continuum: only discrete energy levels \(\omega\) then exist, as determined from the Bethe equations.
Fermions on a lattice
Impurity models
Gaudin magnets
Ground states: identification, properties and excitations
Lieb-Liniger
The thermodynamic limit
The Bethe equations represent a mapping between a proper set of quantum numbers \(\{I_j\}\) and a set of momenta (rapidities) \(\{\lambda_j\}\). This map is nonlinear and fully-coupled: changing one quantum number changes all the rapidities. For nontrivial values of the interaction (namely: \(c\) neither \(0\) nor \(\infty\)), the Bethe equations form a transcendental system of equations which cannot be solved in closed form. As is often the case in statistical mechanics, one can however hope that going to a thermodynamically large system allows to simplify matters somewhat. This chapter provides details of how to implement such a limit.
For large \(L\) and finite quantum number difference, the rapidities \(\lambda_j\) are always separated by intervals of order \(1/L\), as can be seen from inequality l.bd. In the thermodynamic limit, defined as the limit \(L \rightarrow \infty\), \(N \rightarrow \infty\), with \(N/L\) fixed and finite, they become dense on (subsets of) the real line.
Let us begin by considering a given proper set of quantum numbers \(I_j\). Let us then introduce a function \(\lambda(x)\) for an argument \(x\) on the real line \(\mathbb{R}\), which we interpret as a continuum version of the space of quantum numbers. On the discrete set of points \(\left\{ x_j = \frac{I_j}{L} \right\}\), we fix the values of \(\lambda(x)\) to \(\lambda(x_j) = \lambda_j\), the \(\{ \lambda_j \}\) being the solution to the Bethe equations for a given specific proper set \(\{ I_j\}\). The Bethe equations can then be rewritten as
\begin{equation*} \lambda(x_j) + \frac{1}{L} \sum_{l=1}^N \phi(\lambda(x_j) - \lambda(x_l)) = 2\pi x_j. \end{equation*}The value of the function \(\lambda(x)\) remains arbitrary outside of the discrete set of points \(\{ x_j\}\). A natural extension to the whole of \(\mathbb{R}\) can be obtained by requiring that \(\lambda(x)\) fulfill the following equation for any \(x \in \mathbb{R}\),
<<l.bee>>
where we have defined the density distribution
\begin{equation*} \rho (x) = \frac{1}{L} \sum_{j=1}^N \delta (x - \frac{I_j}{L}) \end{equation*}which is exactly determined by the chosen \(\{ I_j \}\). The function \(\lambda(x)\) defined by l.bee is a single-valued, monotonically increasing function of \(x\) associated to a given \(\rho(x)\), and defines a one-to-one mapping \(\mathbb{R} \to \mathbb{R}\).
In particular, l.bee defines the function \(\lambda(x)\) for points \(x = \tilde{I}/L\) with \(\tilde{I} \notin \{I_j \}\), and \(\tilde{I}\) half-odd integer if \(N\) is even and integers if \(N\) is odd (in other words on the unoccupied quantum numbers of the allowed set). The sets \(\{I \}\) and \(\{ \tilde{I} \}\) are complementary, in the sense that \(\{ I \} + \{\tilde{I}\} = \{ T \}\) with \(\{ T \} = {\mathbb Z} + 1/2\) if \(N\) is even and \(\{ T \} = {\mathbb Z}\) if \(N\) is odd. We call particle rapidity a rapidity \(\lambda(\frac{n}{L})\) with \(n \in \{I \}\), and a hole rapidity one with \(n \in \{ \tilde{I} \}\). Particle, hole and total densities are then defined as
<<l.rx>>
In the thermodynamic limit, these densities become smooth functions of \(x\). In particular,
\begin{equation*} \rho_t (x) \rightarrow_{ThLim} \int_{-\infty}^{\infty} dy ~\delta (x - y) = 1. \end{equation*}The continuum version of the Bethe equations l.bex define a continuous differentiable mapping between the \(x\)- and \(\lambda\)-spaces. This allows us to rewrite the densities as functions in \(\lambda\)-space by simply using the transformation rule for \(\delta\) functions (we abuse the notation and use the same symbol, the argument determining which density we are using)
<<l.r>>
We thus rewrite the Bethe equations as
<<l.bex>>
Differentiating with respect to \(\lambda\) gives (using the definition of the fundamental Cauchy kernel l.ck)
\begin{equation*} 1 + 2\pi \int_{-\infty}^{\infty} d\lambda' ~{\cal C} (\lambda - \lambda') \rho (\lambda') = 2\pi (\rho (\lambda) + \rho_h (\lambda)), \end{equation*}or more succinctly
<<l.bec>>
where we have used the convolution notation
<<convo>>
Equation l.bec is a functional relation between two functions. It can thus be interpreted as follows: given any function \(\rho_h (\lambda)\), it determines a function \(\rho(\lambda)\) and thus an eigenstate. Alternately, given a \(\rho(\lambda)\), a \(\rho_h(\lambda)\) can be calculated. Given the distribution \(\rho (\lambda)\), the particle, momentum and energy (linear) densities of the state are
<<l.npe>>
The ground state and the Lieb equation
The ground state is obtained through choosing the following set of quantum numbers:
<<l.igs>>
In the thermodynamic limit, we can immediately obtain an integral equation for the corresponding ground state rapidity density function. We shall look for a ground state with finite particle density \(n\). It is then natural to look for a density \(\rho_g(\lambda)\) which is nonzero only within a finite interval \(\lambda \in [-\lambda_F, \lambda_F]\) such that
<<l.rg>>
The integral equation l.bec therefore becomes
<<l.le>>
which is known as the Lieb equation. The Fermi momentum \(\lambda_F\) can be viewed as an independent variable which (indirectly) specifies the particle density \(n\), the relationship between these being
<<l.ng>>
The density is a monotonically increasing function of \(\lambda_F\) for \(c>0\) (this will be proven later on), but the exact relationship cannot be written in closed form. In practice, one thus needs to solve l.le and l.ng self-consistently if one requires a specific particle density.
The Lieb equation is in fact identical to an equation known as Love's equation, occurring in classical electrostatics, and describing the capacitance of a circular capacitor. It does not admit a closed-form solution for \(0 < c < \infty\). Expansions for small or large interactions can however be written down. See b-Gaudin for details.
Plots of the ground-state rapidity density function \(\rho(\lambda)\) for a number of values of the interaction parameter can be found in Fig. FigLLgs. There, \(k_F\) as a function of \(c\) for unit filling \(n=1\) is also plotted, together with the chemical potential \(\mu\), as well as the total (\(e\)), kinetic (\(t\)) and potential (\(v\)) energy per unit lenght (in other words per particle at unit filling). These are simply calculated as
\begin{equation*} e = t + v, \hspace{10mm} v = c \frac{\partial e}{\partial c}. \end{equation*}It is interesting to define the `maximally complicated' value of interaction for Lieb-Liniger as the point at which the kinetic energy density equals the interaction energy density (there is then no obvious starting point for any perturbative expansion). This occurs when \(t = v \simeq 0.82668(1)\) at \(\gamma \simeq 4.3485(1)\). Note that the interaction energy density has a maximum of \(\simeq 0.8277(1)\) at a slightly higher value of the interaction \(\gamma \simeq 4.6572(4)\), the kinetic energy density then being \(\simeq 0.8824(2)\).
<<FigLLgs>>
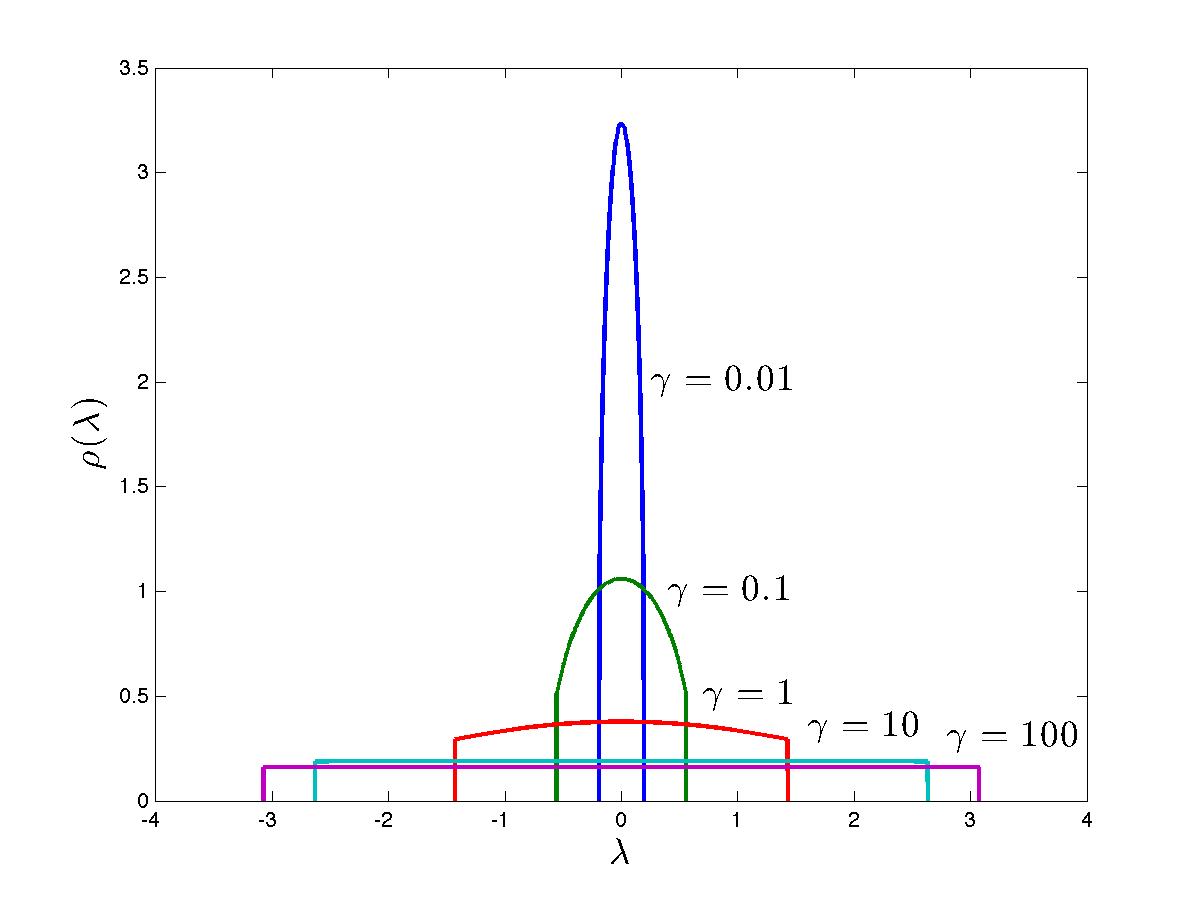 |
 |
 |
 |
The solution of the Lieb equation is particularly simple in the limit \(c \rightarrow \infty\), since the Cauchy kernel vanishes. One then gets
\begin{equation*} \rho(\lambda)|_{c \rightarrow \infty} = \frac{\theta (\lambda_F - |\lambda|)}{2\pi}, \hspace{10mm} \lambda_F = \pi n. \end{equation*}The Bethe equations l.bec then give the very simple hole density \(\rho_h\) and total density \(\rho_t\)
\begin{equation*} \rho_h (\lambda)|_{c \rightarrow \infty} = \frac{\theta (|\lambda| - \lambda_F)}{2\pi}, \hspace{10mm} \rho_t (\lambda)|_{c \rightarrow \infty} = \frac{1}{2\pi}. \end{equation*}Excitations in the vicinity of the ground state
Now that we have provided a certain amount of detail concerning the ground state and the equations which determine it in the thermodynamic limit, we can turn our eye towards other states in the Hilbert space. In view of the Fermi segment structure of the ground state, the most natural procedure is to proceed by analogy with the Fermi gas and construct simple particle-hole excitations.
Particle-like excitations (Type I)
Let us here consider a one-particle excitation over the \(N\)-particle ground state, by constructing the \(N+1\)-particle state with quantum numbers
\begin{equation*} \{ I_j\} = \left\{ -\frac{N}{2}, -\frac{N}{2} + 1, ..., \frac{N}{2} - 1, \frac{N}{2} + m \right\}. \end{equation*}This state has momentum \(P = \frac{2\pi m}{L}\), and we denote its rapidities by the set \(\{ \lambda_1, ..., \lambda_N, q \}\). As compared to the ground state rapidities \(\{ \lambda^0 \}\), the \(\{ \lambda \}\) rapidities will move by a small amount
\begin{equation*} \Delta \lambda_j = \lambda_j - \lambda_j^0 \equiv d_j/L. \label{eq:1DBG:dj} \end{equation*}Explicitly, the Bethe equations for the ground state rapidities \(\{ \lambda_j^0 \}\) and excited state ones \(\{ \lambda_j \}\) are respectively
\begin{align*} &L\lambda_j^0 = 2\pi \left( -\frac{N}{2} - \frac{1}{2} + j \right) - \sum_{l=1}^N \phi (\lambda_j^0 - \lambda_l^0), \nonumber \\ &L\lambda_j = 2\pi \left( -\frac{N}{2} - 1 + j \right) - \sum_{l=1}^N \phi (\lambda_j - \lambda_l) - \phi(\lambda_j - q). \end{align*}The difference \(d_j\) thus obeys the equation
\begin{equation*} d_j = -\pi - \phi(\lambda_j - q) - \sum_{l=1}^N [\phi (\lambda_j - \lambda_l) - \phi(\lambda_j^0 - \lambda_l^0)]. \end{equation*}Since \(\Delta \lambda_j\) is of order \(1/L\), we can write
\begin{equation*} d_j = -\pi - \phi(\lambda_j - q) - \frac{1}{L}\sum_{l=1}^N \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2} (d_j - d_l) + \mbox{O}(N/L^2) \end{equation*}and therefore
\begin{equation*} d_j \left( 1 + \frac{1}{L} \sum_{l=1}^N \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2}\right) = -\pi - \phi(\lambda_j - q) +\frac{1}{L}\sum_{l=1}^N \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2} d_l. \end{equation*}Inserting our definition of the density l.r, and defining the continuous function \(d (\lambda_j, q) = d_j\), we can again extend the definition of \(d(\lambda, q)\) to all \(\lambda\) by taking
\begin{align*} d(\lambda, q) &\left( 1 + 2\pi \int_{-\lambda_F}^{\lambda_F} d\lambda' {\cal C} (\lambda-\lambda') \rho(\lambda') \right) \hspace{20mm} \nonumber \\ &= -\pi - \phi(\lambda - q) + 2\pi \int_{-\lambda_F}^{\lambda_F} d\lambda' {\cal C} (\lambda-\lambda') \rho(\lambda') d(\lambda', q). \end{align*}Introducing the displacement function for Type I particle-like excitations
\begin{equation*} D_p(\lambda, q) = d(\lambda, q) \rho(\lambda) \end{equation*}and making use of the Lieb equation, we get
<<l.d1>>
The change in momentum can be expressed as
<<l.d1p>>
whilst the change in free energy (so taking the chemical potential into account) is
<<l.d1e>>
The type I dispersion relation is illustrated in fig-T1disprel for various values of the interaction parameter, and is contrasted to the free and Bogoliubov dispersions in fig-T1comp for three values of interactions. The approximations are extremely accurate except for strong interactions.
<<fig-T1disprel>>

<<fig-T1comp>>
 |
 |
 |
In the limit \(c \rightarrow 0^+\), we get \(D_p = 0\) and thus (since the chemical potential then goes to zero), the dispersion relation for this type of excitation is
\begin{equation*} \epsilon(p) = p^2, \hspace{0.3cm} c = 0^+. \end{equation*}For \(c \rightarrow \infty\), the solution is \(D_p = -1/2\), so \(\Delta P = q - \lambda_F\) and \(\Delta E = q^2 - \mu\). Since \(\mu = \lambda_F^2\) and \(\lambda_F = \pi n\), we obtain in this case
\begin{equation*} \epsilon(p) = p^2 + 2\pi n p, \hspace{10mm} p > 0, \hspace{0.3cm} c \rightarrow \infty. \end{equation*}These two limits form the lower and upper limits of the particle-like excitations. Type I excitations correspond to Bogoliubov modes.
Hole-like excitations (Type II)
Let us now do the converse of the above: we construct an excited state by now punching a hole in the \(N\) particle ground state, choosing the quantum numbers
\begin{equation*} \{ I_j \} = \left\{ -\frac{N}{2} + 1, ..., \frac{N}{2} - m - 1, \frac{N}{2} - m + 1, ..., \frac{N}{2} \right\}. \end{equation*}We single out the \(I^0 = \frac{N - 1}{2} - m\) quantum number in the ground state interval (viewing \(m\) as being in \(0 < m < \frac{N}{2}\), namely the hole is on the right side of the Fermi interval) and call the associated rapidity \(q\) with restriction \(|q| < \lambda_F\). We therefore have to order \(1/L\)
\begin{equation*} d_j = \pi + \phi (\lambda_j - q) - \frac{1}{L} \sum_{l=1}^{N-1} \frac{2c}{(\lambda_j - \lambda_l)^2 + c^2} (d_j - d_l) \end{equation*}which leads to the following equation for the corresponding displacement:
<<l.d2>>
The change in momentum can be expressed as
<<l.d2p>>
whilst the change in energy is
<<l.d2e>>
The type II dipsersion relation is illustrated in Fig. fig-T2disprel for various values of the interaction parameter.
<<fig-T2disprel>>

In the limit \(c \rightarrow 0^+\), we get \(\epsilon(p) = 0\).
For \(c \rightarrow \infty\), the solution is \(D_h = 1/2\), so \(\Delta P = - q + \lambda_F\) and \(\Delta E = -q^2 + \mu\). Since \(\mu = \lambda_F^2\) and \(\lambda_F = \pi n\), we obtain in this case
\begin{equation*} \epsilon(p) = -p^2 + 2\pi n p, \hspace{0.3cm} c \rightarrow \infty, \hspace{5mm} p \in [0, 2 \pi n]. \end{equation*}These two limits form the lower and upper limits of the hole-like excitations.
Heisenberg
Going to infinite size
The Bethe equations h.bel represent a mapping between sets of quantum numbers \(\{ I_a \}\) and sets of rapidities \(\{ \lambda_a \}\). The nonlinearity of this mapping, together with its fully-coupled nature (any single rapidity is an implicit function of all the quantum numbers) mean that there is no universally robust algorithm to generate the solutions of the Bethe equations. Nevertheless, some analytical results can be obtained by going to the thermodynamic limit.
We proceed as follows. Consider a set of rapididites \(\{ \lambda_a \}\), solution to the Bethe equations for a set \(\{ I_a \}\) of quantum numbers. For simplicity, we consider \(\lambda_a \in {\mathbb R}\) for the moment. Let us first introduce a function \(\lambda(x)\) of a real parameter \(x\), having the property that it takes the value of the rapidity \(\lambda_a\) when evaluated at argument \(I_a/N\), \(\lambda(I_a/N) = \lambda_a\) for \(a = 1, ..., M\). Second, let us introduce a density function
\begin{equation*} \rho(x) = \frac{1}{N} \sum_{a=1}^M \delta (x - I_a/N) \end{equation*}which is again fully specified by the given eigenstate. The Bethe equations h.bel can now be written
\begin{equation*} \left(\phi_1 (\lambda(x)) - \int_{-x_-}^{x_+} dy~\phi_2(\lambda(x) - \lambda(y)) \rho(y) - 2\pi x\right) |_{x = I_a/N} = 0, \end{equation*}where \(x_+\) and \(x_-\) are real numbers.% such that \(\rho(x > x_+) = \rho(x < -x_-) = 0\).
The following step is to generalize this to the whole real axis of the \(x\) variable. That is, we pose that the value of \(\lambda(x)\) for any \(x \in \mathbb{R}\) is given by the solution to the integral equation
<<h.bee>>
In particular, for a given \(\rho(x)\), this defines \(\lambda(x)\) on the set of points \(x = \bar{I}/N\) defined by the complementary quantum numbers (in other words, the unoccupied quantum numbers) \(\{ \bar{I} \}]\) defined by \(\{ I \} + \{\bar{I}\} = \{ T \}\) with \(\{ T \} = \mathbb{Z} + 1/2\) if \(N - M\) is even and \(\{ T \} = \mathbb{Z}\) if \(N - M\) is odd. We call particle quantum number an occupied quantum number, and hole quantum number an unoccupied one. Densities of particles and holes can now be defined in \(x\)-space:
\begin{equation*} \rho(x) = \frac{1}{N} \sum_{n \in \{I\}} \delta (x - \frac{n}{N}), \hspace{0.5cm} \rho_h(x) = \frac{1}{N} \sum_{m \in \{\bar{I}\}} \delta (x - \frac{m}{N}), \end{equation*}as well as the total (sum of particle and hole) density
\begin{equation*} \rho_t (x) = \rho (x) + \rho_h (x). \end{equation*}In the thermodynamic limit \(N \rightarrow \infty\), the densities become smooth functions. In particular, the total density becomes
\begin{equation*} \rho_t (x) \rightarrow_{T.L.} \int_{-\infty}^{\infty} dy ~\delta (x - y) = 1. \end{equation*}The continuum extension of the Bethe equations, l.bee defines \(\lambda(x)\) as a mapping from \(x\)-space to rapidity space. We suppose that this mapping is invertible, in other words that the function \(x(\lambda)\) exists and is differentiable. We can rewrite the three densities in rapidity space by using the transformation rules for delta functions (we abuse notations and use the same symbol),
\begin{align*} \rho (\lambda) &= \rho (x(\lambda)) \frac{d x(\lambda)}{d\lambda}, \\ \rho_h (\lambda) &= \rho_h (x(\lambda)) \frac{d x(\lambda)}{d\lambda}, \\ \rho_t (\lambda) &= \rho_t (x(\lambda)) \frac{d x(\lambda)}{d\lambda} = \frac{ d x(\lambda)}{d\lambda}, \end{align*}with \(\rho (\lambda) + \rho_h (\lambda) = \rho_t (\lambda)\). This allows us to rewrite l.bee as
\begin{equation*} \phi_1 (\lambda) - \int_{-\lambda_-}^{\lambda_+} d\lambda' ~\phi_2(\lambda - \lambda') \rho(\lambda') = 2\pi x(\lambda) \end{equation*}where \(\lambda_{\pm} = \lambda(x_{\pm})\). Differentiating this equation with respect to \(\lambda\), and defining the differential kernels \(a_n\) as
<<h.an>>
yields the integral equation
<<h.bec>>
linking the particle and hole densities of Bethe eigenstates. In other words: this equation should be interpreted as the continuum limit of the Bethe equations for a particular eigenstate, whose distribution of rapidities is given by the density function \(\rho(\lambda)\).
The energy and momentum of a state with rapidity distribution \(\rho(\lambda)\) is readily obtained in view of the definition of the density:
<<h.ep>>
The ground state of the infinite isotropic antiferromagnet
The ground state is characterized by a fully-packed distribution of quantum numbers, symmetric with respect to \(\lambda = 0\). The limits \(\lambda_{\pm}\) are thus equal to a magnetization-dependent constant \(\lambda_F\). For \(|\lambda| < \lambda_F\), the hole density identically vanishes, while the particle density vanishes for \(|\lambda| > \lambda_F\). The continuum Bethe equation l.bec therefore becomes an equation for the single root distribution \(\rho_g(\lambda)\),
<<h.rge>>
which is the \(XXX\) version of the Lieb equation l.le.
For nonzero magnetization, the boundaries \(\lambda_F\) are finite. However, as the magnetic field goes to zero, \(h \rightarrow 0^+\), we have that \(\lambda_F \rightarrow \infty\) as can be seen from the discussion on limiting quantum numbers in c_h_e_rr. In this zero field case (and this case only), h.rge can be solved using the convolution theorem. We define Fourier transforms as
<<h.f>>
The kernels \(a_n (\lambda)\) then have the Fourier transforms
<<h.anf>>
The convolution theorem used in h.rge thus allows to immediately solve for the zero-field ground state root distribution \(\rho_g\) \[ \rho_g (\omega) = \frac{a_1(\omega)}{1 + a_2(\omega)} = \frac{1}{2\cosh \omega/2}, \]
Poles at \(\omega_n = 2\pi i (n + 1/2)\), \(n = 0, 1, ...\) in UHP (close there for \(\lambda < 0\)). Residues:
\begin{equation*} \frac{d}{d\omega} \cosh \frac{\omega}{2} = \frac{1}{2} \sinh \omega \end{equation*}whose inverse Fourier transform gives the distribution in rapidity space:
<<h.rg>>
The ground-state energy 1938.Hulthen.AMAF.26A and momentum can thus be computed exactly by substituting h.rg in h.ep,
<<h.epg>>
Excitations at zero field: spinons
Besides the zero-field ground state, it is possible to analytically construct eigenstates with finite numbers of excitations. We consider here the simplest type of excited states, which are obtained by upturning one of the down spins and considering purely real, finite rapidity solutions to the Bethe equations.
Let us begin again with the finite lattice of an even number \(N\) of sites. We specialize to the subsector with \(M = N/2 - 1\) downturned spins. According to h.im, the maximal allowable quantum number for real finite rapidities is then \(I^{\mbox{max}}_{N/2-1} = N/4\). Since we must put \(M = N/2 - 1\) particles in \(2I^{\mbox{max}}_{N/2-1} + 1 = N/2 + 1\) available slots, we can construct
\begin{equation*} N_{2sp} = \frac{N(N+2)}{8} \end{equation*}different states, which will be called 2-spinon states 1981.Faddeev.PLA.85. The set of quantum numbers of these states are completely characterized by the position of the two holes in the quantum number distribution, which we write \(I^h_1, I^h_2\). The presence of these holes means that we can write the \(x\)-space hole distribution as \(\rho_h(x) = \frac{1}{N} \delta(x - \frac{I^h_1}{N}) + \frac{1}{N} \delta(x - \frac{I^h_2}{N})\). By defining the hole rapidities \(\lambda^h_i = \lambda(x = I^h_i/N)\), this distribution becomes \[ \rho_h (\lambda) = \frac{1}{N} \delta(\lambda - \lambda^h_1) + \frac{1}{N} \delta(\lambda - \lambda^h_2) \] in rapidity space. Equation l.bec for a 2-spinon state labeled by hole rapidities \(\lambda^h_i\) thus becomes \[ a_1(\lambda) = \rho(\lambda) + a_2 * \rho(\lambda) + \frac{1}{N} \delta(\lambda - \lambda^h_1) + \frac{1}{N} \delta(\lambda - \lambda^h_2) \] where the convolution notation is \(a * b (\lambda) = \int_{-\infty}^{\infty} d\lambda' a(\lambda - \lambda') b(\lambda')\). Fourier transforming gives \[ \rho_{\rm 2sp}(\omega; \lambda^h_1, \lambda^h_2) = \rho_g (\omega) - \frac{\rho_{\rm sp} (\omega)}{N} (e^{i\omega\lambda^h_1} + e^{i\omega\lambda^h_2}), \] where \(\rho_g (\omega)\) is the ground state rapidity distribution and \(\rho_{\rm sp} (\omega) = \frac{1}{1 + a_2 (\omega)} = \frac{1}{1 + e^{-|\omega|}}\) is the spinon density function. The inverse Fourier transform finally yields
\begin{equation*} \rho_{\rm 2sp} (\lambda; \lambda^h_1, \lambda^h_2) = \rho_g (\lambda) - \frac{1}{N} \rho_{\rm sp} (\lambda - \lambda^h_1) - \frac{1}{N} \rho_{\rm sp} (\lambda - \lambda^h_2) \end{equation*}where the spinon density distribution is given in terms of the Dirac delta distribution corrected by reals part of digamma functions:
<<h.r2sp>>
Knowing the rapidity distribution, we can now compute the energy and momentum of a 2-spinon state over that of the ground state:
\begin{equation*} E_{\rm 2sp} (\lambda^h_1, \lambda^h_2) = -NJ\pi \int_{-\infty}^{\infty} d\lambda a_1 (\lambda) [\rho_{\rm 2sp} (\lambda; \lambda^h_1, \lambda^h_2) - \rho_g (\lambda)] \end{equation*}meaning that
<<h.2spe>>
where the single spinon energy is
\begin{equation*} \varepsilon_{\rm sp} (\lambda^h) = J \pi \int_{-\infty}^{\infty} d\lambda a_1 (\lambda) \rho_{\rm sp} (\lambda - \lambda^h) = J\pi \int_{-\infty}^{\infty} \frac{d\omega}{2\pi} a_1 (\omega) \rho_{\rm sp}(\omega) e^{i\omega \lambda^h} = \frac{J\pi}{2\cosh \pi \lambda^h}. \end{equation*}The momentum of the 2-spinon state over that of the ground state is similarly expressed as
<<h.2spp>>
where \[ p_{\rm sp} (\lambda^h) = -\int_{-\infty}^{\infty} d\lambda \rho_{\rm sp} (\lambda - \lambda^h) [\pi - \phi_1 (\lambda)]. \] We have that \(\lim_{\lambda^h \rightarrow \infty} p_{\rm sp} (\lambda^h) = 0\), and \[ \frac{dp_{\rm sp}}{d\lambda^h} = 2\pi \int_{-\infty}^{\infty} d\lambda \rho_{\rm sp} (\lambda) a_1 (\lambda) = 2\varepsilon_{\rm sp} (\lambda^h)/J, \] which allows to write \[ p_{\rm sp} (\lambda^h)= -\int_{\lambda^h}^{\infty} d\lambda \frac{\pi}{\cosh \pi \lambda} = - 2~\mbox{atan} (e^{-\pi \lambda^h}) ~~\in [-\pi, 0]. \] In turn, back-substitution into the single spinon energy yields the well-known spinon dispersion relation
<<h.esp>>
Further spin chains
The planar Heisenberg chain
The ground state of the planar antiferromagnet
Calculations for the ground state of the infinite XXZ antiferromagnet completely parallel those done for the isotropic case. The differential kernel is here
<<p.an>>
Instead of h.anf, we thus get
<<p.anf>>
For zero field, we again have \(\lambda_F \rightarrow \infty\); the convolution theorem therefore allows to solve the continuum Bethe equations h.rg for the ground state root density distribution,
<<p.rg>>
The ground state energy and momentum can again be calculated by substituting this distribution back into h.ep, yielding 1966.desCloizeaux.JMP.7.1
<<p.epg>>
Excitations at zero field: XXZ spinons
Similarly as for the isotropic case, we obtain \(\rho_{\rm sp} (\omega) = \frac{1}{1 + a_2 (\omega)}\) so
<<p.rsp>>
The energy and momentum of 2-spinon states are again given by h.2spe and h.2spp (using the XXZ kernels), where the single spinon energy and momentum here become
\begin{equation*} \varepsilon_{\rm sp} (\lambda^h) = \frac{J \pi \sin \zeta}{2\zeta \cosh (\frac{\pi \lambda^h}{\zeta})}, \hspace{1cm} p_{\rm sp} (\lambda^h) = -2~\mbox{atan} ~e^{-\pi \lambda^h/\zeta} \in [-\pi, 0]. \end{equation*}Combining these gives the XXZ spinon dispersion relation,
<<p.esp>>
Equilibrium at finite \(T\): the Thermodynamic Bethe Ansatz
Lieb-Liniger
Yang-Yang formalism; Gibbs free energy
According to the basic principles of statistical mechanics, for arbitrary temperatures, equilibrium properties are encoded in the partition function. Since the Hilbert space is spanned by the Bethe eigenfunctions, which are in turn catalogued by a set of sets of quantum numbers \(\{ \{ I \} \}\), we can formally write the partition function in the grand-canonical Gibbs ensemble with chemical potential \(\mu \in \mathbb{R}\) as
\begin{equation*} {\cal Z} = \mbox{Tr} e^{-(E - \mu N)/T} = \sum_{N=0}^\infty \sum_{\{ I \}_N} e^{-(E_{\{ I \}_N} - \mu N)/T} \end{equation*}in which \(\{ I \}_N\) represents a proper set of quantum numbers at fixed particle number \(N\).
We shall now transform the explicit summation over all possible configurations of quantum numbers into a functional integral. In order to do this, imagine partitioning the real line for our quantum number coordinate \(x\) into `boxes' \(B_\alpha \equiv [x_\alpha, x_\alpha + \Delta x_\alpha \equiv x_{\alpha+1}]\), \(\alpha \in \mathbb{Z}\), each segment width \(\Delta x_\alpha\) being such that \(\frac{1}{L} \ll \Delta x_\alpha \ll 1\). In each such segment, for each individual eigenstate specified by our densitites l.rx, there are
\begin{align*} L \rho_t (x_\alpha) \Delta x_\alpha ~~ &\mbox{allowed slots, with} \nonumber \\ L \rho (x_\alpha) \Delta x_\alpha ~~~ &\mbox{particles and} \nonumber \\ L \rho_h (x_\alpha) \Delta x_\alpha ~~ &\mbox{holes,} \end{align*}where the densities obey the constraints \(\rho_t (x) = \rho(x) + \rho_h(x)\) with \(0 \leq \rho (x) \leq 1\), and \(\rho_t (x) \rightarrow 1\) upon taking the thermodynamic limit. We can then rewrite our summation over quantum number configurations as
\begin{equation*} \sum_{N=0}^\infty \sum_{\{ I\}_N} (...) = \prod_{\alpha = -\infty}^\infty ~~\sum_{n_\alpha = 0}^{L\Delta x_\alpha} ~~\sum_{\{ \frac{I}{L}\}_{n_\alpha} \in B_\alpha} (...). \end{equation*}Let us now exploit the fact that the energy and particule number densities become smooth functionals of \(\rho(x)\) upon taking the thermodynamic limit. This means that performing "in-box" shufflings of quantum numbers in each individual segment \(\Delta x_\alpha\) does not affect the value of the Gibbs weight to leading order. As far as the partition function is concerned, we can thus write a parenthesis around the in-box summation and perform it explicitly:
<<l.ibs>>
By assumption, \(\Delta x_\alpha\) is such that all numbers in square brackets are very large as compared to one. We can thus invoke Stirling's approximation
\begin{equation*} \ln (P!) = P \ln P - P + \frac{1}{2} \ln (2\pi P) + O(1/P) \end{equation*}and rewrite the right-hand side of l.ibs as
\begin{equation*} e^{S_\alpha L \Delta x_\alpha}, \hspace{10mm} S_\alpha \equiv (\rho(x_\alpha) + \rho_h(x_\alpha)) \ln (\rho(x_\alpha) + \rho_h(x_\alpha)) - \rho(x_\alpha) \ln \rho(x_\alpha) - \rho_h(x_\alpha) \ln \rho_h (x_\alpha). \end{equation*}Applying this logic to all boxes \(B_\alpha\) then leads us to the rewriting of our summation over quantum number configurations (provided the summand \((...)\) is blind to in-box shufflings of quantum numbers) as a functional integral weighed by an entropy functional,
\begin{align*} &\sum_{N=0}^\infty \sum_{\{ I\}_N} (...) \rightarrow \int {\cal D} [\rho(x)] e^{S[\rho(x)]} (...), \nonumber \\ &S[\rho(x)] \equiv L \int_{-\infty}^\infty dx \left[ (\rho(x) + \rho_h (x)) \ln (\rho(x) + \rho_h(x)) - \rho (x) \ln \rho(x) - \rho_h(x) \ln \rho_h(x) \right], \hspace{5mm} \nonumber \end{align*}(note that we could simplify our expression for the entropy by using the fact that \(\rho(x) + \rho_h(x) \rightarrow 1\); we leave it as it is for later clarity), where the functional integral is viewed as the integral over the possible fillings of infinitely many boxes with in-box densities \(\rho (x_\alpha) \equiv \rho_\alpha\),
<<l.fix>>
Our partition function is thus represented as
<<l.zx>>
In our considerations, we have however found it convenient to work with densities in rapidity space rather than quantum number space. We can thus formally perform a functional transformation \(\rho(x), \rho_h(x) \rightarrow \rho(\lambda), \rho_h(\lambda)\) and rewrite our partition function in the grand canonical ensemble as a functional integral over the densities \(\rho(\lambda), \rho_h(\lambda)\), modulo imposition of the Bethe equations:
<<l.zl>>
where the functional integral should be read as
\begin{align*} \int {\cal D} [\rho(\lambda), \rho_h(\lambda)] &\left. (...) \right|_{\rho + \rho_h = \frac{1}{2\pi} + {\cal C} * \rho} \equiv \\ &\int {\cal D} [\rho(\lambda)] {\cal D} [\rho_h(\lambda)] ~\mbox{Det} \left[ \frac{\delta \rho(x)}{\delta \rho(\lambda)}\right] \delta (\rho + \rho_h - {\cal C} * \rho - \frac{1}{2\pi}) (...), \end{align*}the Jacobian being interpreted as a Fredholm determinant. Note that we are being cavalier with some subtleties: the precise definition of the measures \({\cal D} [\rho(\lambda)]\) and \({\cal D}[\rho_h(\lambda)]\) parallels l.fix but has nontrivial (interaction- and state-dependent) upper limits of the individual integrals. One should thus view our version l.zl as a mere notational convenience, and see l.zx as the properly-defined version on which one should fall back in case of doubt.
The extensive particle number and energy are
\begin{equation*} N[\rho] = L \int_{-\infty}^{\infty} d\lambda ~\rho(\lambda), \hspace{10mm} E[\rho] = L \int_{-\infty}^{\infty} d\lambda ~\lambda^2 ~\rho(\lambda) \end{equation*}and the entropy reads
\begin{equation*} S[\rho,\rho_h] = L \int_{-\infty}^{\infty} d\lambda \left( [\rho(\lambda) + \rho_h(\lambda)] \ln [\rho(\lambda) + \rho_h(\lambda)] \!-\! \rho(\lambda) \ln \rho(\lambda) \!-\! \rho_h(\lambda) \ln \rho_h (\lambda) \right). \end{equation*}Simplifying notations somewhat, we write the partition function in the grand-canonical ensemble as the functional integral
\begin{equation*} {\cal Z} = \int \left. {\cal D} [\rho(\lambda),\rho_h(\lambda)] e^{-G[\rho,\rho_h]/T}\right|_{\rho + \rho_h = \frac{1}{2\pi} + {\cal C} * \rho}, \end{equation*}with Gibbs weight
\begin{align*} G[\rho,\rho_h] = L \int_{-\infty}^{\infty} d\lambda \left\{ \rho(\lambda) \left[ \lambda^2 - \mu - T \ln [\rho(\lambda) + \rho_h(\lambda)] + T \ln \rho(\lambda)\right] + \right. \nonumber \\ \left. + ~\rho_h(\lambda) \left[ - T \ln [\rho(\lambda) + \rho_h(\lambda)] + T \ln \rho_h(\lambda)\right] \right\}. \end{align*}In the limit \(L \rightarrow \infty\), this functional integral can be evaluated in a saddle-point approximation. To quantify this, we perform the variations
\begin{align*} \rho(\lambda) &\rightarrow \rho(\lambda) + \delta \rho(\lambda), \nonumber \\ \rho_h(\lambda) &\rightarrow \rho_h(\lambda) + \delta \rho_h (\lambda). \end{align*}This gives
\begin{align*} \frac{\delta G}{L} = \int_{-\infty}^{\infty} d\lambda \left\{ \delta \rho(\lambda) \left[ \lambda^2 -\mu - T\ln[\rho + \rho_h] + T \ln \rho \right] + \rho \left[ -T \frac{\delta \rho + \delta \rho_h}{\rho + \rho_h} + T \frac{\delta \rho}{\rho} \right] \right. \nonumber \\ \left. + \delta \rho_h \left[ -T \ln [\rho + \rho_h] + T \ln \rho_h \right] + \rho_h \left[ -T \frac{\delta \rho + \delta \rho_h}{\rho + \rho_h} + T \frac{\delta \rho_h}{\rho_h} \right] \right\} \end{align*}which simplifies to
\begin{equation*} \frac{\delta G}{L} = \int_{-\infty}^{\infty} d\lambda \left\{\delta \rho \left[\lambda^2 - \mu - T \ln [1 + \rho_h/\rho]\right] + \delta \rho_h [-T \ln [1 + \rho/\rho_h]] \right\}. \end{equation*}The variations \(\delta \rho\) and \(\delta \rho_h\) are not independent. They are related by equation l.bec,
\begin{equation*} \delta \rho(\lambda) - {\cal C} * \delta \rho(\lambda) = -\delta \rho_h (\lambda). \end{equation*}Substituting this in gives
\begin{equation*} \frac{\delta G}{L} = \int_{-\infty}^{\infty} d\lambda \delta \rho(\lambda) \left[ \lambda^2 - \mu - T \ln \frac{\rho_h(\lambda)}{\rho(\lambda)} - {\cal C} * T \ln \left[1 + \rho(\lambda)/\rho_h(\lambda)\right] \right]. \end{equation*}Since this must vanish for any choice of the variation \(\delta \rho(\lambda)\), we obtain the saddle-point condition
\begin{equation*} T \ln \frac{\rho_h(\lambda)}{\rho(\lambda)} = \lambda^2 - \mu - {\cal C} * T \ln \left[1 + \rho(\lambda)/\rho_h(\lambda)\right]. \end{equation*}We define the function
\begin{equation*} \epsilon (\lambda) = T \ln \frac{\rho_h(\lambda)}{\rho(\lambda)} \end{equation*}whose physical meaning is to represent the energy of fundamental excitations. This gives
\begin{equation*} \epsilon(\lambda) = \lambda^2 - \mu -{\cal C} * T\ln [1 + e^{-\epsilon(\lambda)/T}], \end{equation*}and the free energy density becomes
\begin{align*} \frac{G}{L} &= \int_{-\infty}^{\infty} d\lambda \left\{ \rho(\lambda) \left[ \lambda^2 -\mu - \epsilon(\lambda) \right] - [\rho(\lambda) + \rho_h(\lambda)] T \ln [1 + e^{-\epsilon(\lambda)}] \right\} \nonumber \\ &= \int_{-\infty}^{\infty} d\lambda \left\{ \rho(\lambda) {\cal C} * T \ln [1 + e^{-\epsilon(\lambda)/T}] - T ({\cal C} * \rho (\lambda)) \ln [1 + e^{-\epsilon (\lambda)/T}] \right\} - \frac{T}{2\pi} \int_{-\infty}^{\infty} d\lambda \ln [1 + e^{-\epsilon(\lambda)/T}]. \end{align*}Simple manipulations show that the first two terms cancel, so we are left with the rather simple result
<<l.g>>
where the energy function is solution to
<<l.e>>
This encodes all the equilibrium thermodynamics of the infinite system.
 |
 |
Thermodynamic properties
The pressure is defined as the derivative of the free energy with respect to volume at fixed \(T\):
<<l.pr>>
The isothermal and isoentropic (adiabatic) bulk moduli \(\kappa_T\) and \(\kappa_S\) are defined as
\begin{equation*} \kappa_{T,S} = -L \left( \frac{ \partial P}{\partial L}\right)_{T,S} = n \left( \frac{\partial P}{\partial n} \right)_{T,S}. \end{equation*}The isothermal and isoentropic compressibilities \(\beta_{T,S}\) are the inverses of the bulk moduli,
\begin{equation*} \frac{1}{\beta_{T,S}} = \kappa_{T,S} = -L \left( \frac{\partial P}{\partial L} \right)_{T,S}. \end{equation*}The speed of sound is defined macroscopically as (note: the factor of 2 comes from our conventions, in which we put the mass of the particles to \(1/2\))
<<l.vs>>
The \(c \rightarrow \infty\) (Tonks-Girardeau) limit
We consider here first the limit of infinitely strong interactions, \(c \rightarrow \infty\), which is also known as the Tonks-Girardeau limit. We have that our Cauchy kernel l.ck trivializes to
\begin{equation*} \lim_{c \rightarrow \infty} {\cal C} (\lambda) = 0 \end{equation*}so
\begin{equation*} \epsilon(\lambda) = \lambda^2 - \mu. \end{equation*}The free energy becomes
\begin{equation*} g (T, \mu) = -T \int_{-\infty}^{\infty} \frac{d\lambda}{2\pi} \ln \left[ 1 + e^{-(\lambda^2 - \mu)/T}\right] \end{equation*}and the density
\begin{equation*} \rho(\lambda) + \rho_h(\lambda) = \frac{1}{2\pi} = \rho(\lambda) [1 + e^{(\lambda^2 -\mu)/T}], \end{equation*}so
\begin{equation*} \rho(\lambda) = \frac{1}{2\pi} \frac{1}{e^{(\lambda^2 - \mu)/T} + 1} \end{equation*}which are the same formulas as for free spinless fermions.
The \(c \rightarrow 0^+\) limit
We can also consider the limit \(c \rightarrow 0^+\). Here,
\begin{equation*} \lim_{c \rightarrow 0+} {\cal C} (\lambda) = \delta (\lambda) \end{equation*}so
\begin{equation*} \epsilon(\lambda) = \lambda^2 - \mu - T \ln [1 + e^{-\epsilon(\lambda)/T}], \hspace{10mm} \\ \epsilon(\lambda) = T \ln [e^{(\lambda^2 - \mu)/T} - 1] \end{equation*}and therefore
\begin{equation*} \rho(\lambda) = \frac{1}{2\pi} \frac{1}{e^{(\lambda^2 - \mu)/T} - 1}, \hspace{10mm} \rho_h(\lambda) = \frac{1}{2\pi} \end{equation*}and the free energy
\begin{equation*} g(T, \mu) = T \int_{-\infty}^{\infty} \frac{d\lambda}{2\pi} \ln \left[ 1 - e^{-(\lambda^2 - \mu)/T}\right] \end{equation*}coincides (as expected) with that of ideal free bosons.
Heisenberg
Equations for the thermal equilibrium state
Let us now apply the formalism of the thermodynamic Bethe Ansatz to the isotropic antiferromagnet. Recall the BGT equations h.bgtl:
\begin{equation*} \phi_j (\lambda^j_\alpha) - \frac{1}{N} \sum_{k=1}^{N_s} \sum_{\beta = 1}^{M_k} \Phi_{jk} (\lambda^j_\alpha - \lambda^k_\beta) = \frac{2\pi}{N} I^j_\alpha \end{equation*}with fundamental kernels h.phin
\begin{equation*} \phi_n(\lambda) = 2\mbox{atan} \frac{2\lambda}{n} \end{equation*}and the string-string scattering phase shift h.phijk
\begin{equation*} \Phi_{jk} (\lambda) = (1 - \delta_{jk}) \phi_{|j-k|} (\lambda) + 2\phi_{|j-k|+2} (\lambda) + ... + 2\phi_{j+k-2} (\lambda) + \phi_{j+k} (\lambda). \end{equation*}We will make use of the derivative kernels h.an
\begin{equation*} a_n (\lambda) = \frac{1}{2\pi} \frac{d}{d\lambda}\phi_n(\lambda) = \frac{1}{2\pi} \frac{n}{\lambda^2 + n^2/4}, \hspace{10mm} a_0 (\lambda) \equiv \delta (\lambda) \end{equation*}and
<<h.anm>>
In terms of these, the Bethe equations take the form
\begin{equation*} a_n (\lambda) = \rho_n (\lambda) + \rho_n^h (\lambda) + \sum_{m=1}^\infty A_{nm} * \rho_m (\lambda). \end{equation*}The energy of a state with distributions \(\rho_n (\lambda)\) of \(n\)-strings, \(n = 1, 2, 3, \ldots\) is given by
\begin{equation*} \frac{E}{N} = -\frac{h}{2} + \sum_{n=1}^\infty \int_{-\infty}^\infty d\lambda ~d_n (\lambda) \rho_n (\lambda) \end{equation*}where we have defined the driving term
\begin{equation*} d_n (\lambda) = hn - \pi J a_n (\lambda). \end{equation*}This comes from coupling the external field \(h\) to the total \(z\) projection of spin,
\begin{equation*} \frac{S^z_{tot}}{N} = \frac{1}{2} - \sum_{n=1}^\infty \int_{-\infty}^\infty d\lambda ~n \rho_n (\lambda). \end{equation*}The Yang-Yang entropy of the state is given by
\begin{equation*} \frac{S}{N} = \sum_{n=1}^\infty \int_{-\infty}^\infty d\lambda \left[ (\rho_n + \rho_n^h) \ln (\rho_n + \rho_n^h) - \rho_n \ln \rho_n - \rho_n^h \ln \rho_n^h \right]. \end{equation*}The free energy density per site can thus be written
\begin{equation*} f = \frac{E - TS}{N} = -\frac{h}{2} + \sum_{n=1}^\infty \int_{-\infty}^\infty d\lambda \left[d_n \rho_n - T (\rho_n + \rho_n^h) \ln (\rho_n + \rho_n^h) + T \rho_n \ln \rho_n + T \rho_n^h \ln \rho_n^h \right]. \end{equation*}The variation of this free energy is written as
\begin{equation*} \delta f = \sum_{n=1}^\infty \int_{-\infty}^\infty d\lambda \left\{ \left[ d_n - T \ln (1 + \rho_n^h/\rho_n) \right] \delta \rho_n - T \ln (1 + \rho_n/\rho_n^h) \delta \rho_n^h \right\}. \end{equation*}The variations \(\delta \rho_n\) and \(\delta \rho_n^h\) are however not independent, but linked by the following constraint (from the Bethe equations):
\begin{equation*} \delta \rho_n^h (\lambda) = -\delta \rho_n (\lambda) - \sum_{m=1}^\infty A_{nm} * \delta \rho_m (\lambda). \end{equation*}Substituting this into \(\delta f\) and using the fact that \(A_{nm} = A_{mn}\), we obtain
\begin{equation*} \delta f \!=\! \sum_{n=1}^\infty \int_{-\infty}^\infty \!\!d\lambda ~\delta \rho_n (\lambda) \left[ d_n (\lambda) - T \ln (\rho_n^h (\lambda)/\rho_n(\lambda)) + \sum_{m=1}^\infty A_{nm} \!*\! T \ln \left[ 1 + \rho_m(\lambda)/\rho_m^h(\lambda) \right] \right]. \end{equation*}The condition of thermodynamic stability leads to the requirement that the expression in square brackets vanish for all \(\lambda\). Using the notation
\begin{equation*} \eta_n (\lambda) \equiv \rho_n^h (\lambda)/\rho_n (\lambda), \end{equation*}thermodynamic equilibrium thus imposes the conditions
<<h.tba1>>
The equilibrium value of the free energy itself can now be calculated, explicitly using the Bethe equations to write \(\rho^h\) in terms of \(\rho's\). The result is
\begin{align*} f = -\frac{h}{2} + &\sum_{n=1}^\infty \int_{-\infty}^\infty d\lambda ~\times \nonumber \\ &\left\{-T \ln (1 + \eta_n^{-1} (\lambda)) a_n (\lambda) + \left[ d_n - T \ln \eta_n + \sum_m A_{nm} * T \ln (1 + \eta_m^{-1} (\lambda)) \right] \right\}. \end{align*}Noticing that the term in square brackets vanishes due to the equilibrium condition, we finally get the substantially more concise form
<<h.fn>>
This can be further rewritten in the following way. Starting from the \(n=1\) case of the Bethe equations,
\begin{equation*} \ln (1 + \eta_1 (\lambda)) = \frac{h - \pi J a_1 (\lambda)}{T} + \sum_{m=1}^\infty (a_{m-1} + a_{m+1}) * \ln (1 + \eta_m^{-1} (\lambda)), \end{equation*}and operating \(\int_{-\infty}^\infty d\lambda s(\lambda)\) on this (with \(s(\lambda) = \frac{1}{2\cosh \pi \lambda}\)), we obtain
\begin{equation*} \int_{-\infty}^\infty d\lambda s(\lambda) \ln (1 + \eta_1 (\lambda)) = \frac{h}{2T} - \frac{\pi J}{T} \int_{-\infty}^\infty d\lambda s(\lambda) a_1 (\lambda) + \sum_{m=1}^\infty a_m (\lambda) \ln (1 + \eta_m^{-1} (\lambda)). \end{equation*}Substituting this in the free energy (recognizing the ground-state energy in the second term on the right-hand side) gives the yet more economical form
<<h.f1>>
Factorized form of TBA equations
The fundamental set of TBA equations h.tba1 fully determine the thermal equilibrium state of the \(XXX\) chain at given magnetic field and temperature. Their form is however slightly inconvenient if one thinks of an actual calculation (for example, a numerical solution) due to the fact that all functions are coupled to all others. The coupling kernel \(A_{nm}\) is however relatively simple, being given by a relatively simple sum of fundamental kernels. Inverting this kernel might then yield worthwhile simplifications.
Fourier transforms of kernels
Using the Fourier space expression of our fundamental kernel
\begin{equation*} a_n (\omega) = e^{-\frac{|\omega|}{2} n} \end{equation*}and the definition of the string-string derivative kernel
\begin{equation*} A_{nm} (\omega) = (1 - \delta_{nm}) a_{|n-m|} (\omega) + 2 a_{|n-m|+2} (\omega) + ... + 2 a_{n+m-2} (\omega) + a_{n+m} (\omega), \end{equation*}we obtain
\begin{equation*} A_{n m} (\omega) = \coth \frac{|\omega|}{2} \left( e^{-\frac{|\omega|}{2}|n-m|} - e^{-\frac{|\omega|}{2}(n+m)}\right) - \delta_{nm}. \end{equation*}For future convenience, let us define a kernel inverting \(\delta_{nm} + A_{nm}\). One can verify by direct substitution that the following inversion identity holds:
<<h.b1>>
where
<<h.bnm>>
in which we used
<<h.s>>
We have
\begin{equation*} A_{n+1 m} (\omega) + A_{n-1 m} (\omega) = \coth \frac{|\omega|}{2} \left( e^{-\frac{|\omega|}{2} |n-m + 1|} + e^{-\frac{|\omega|}{2} |n-m-1|} - e^{-\frac{|\omega|}{2} (n+m)} 2\cosh \frac{\omega}{2} \right) \end{equation*}The term in parentheses is
\begin{equation*} = \left\{ \begin{array}{ll} 2\cosh \frac{\omega}{2} \left( e^{-\frac{|\omega|}{2}|n-m|} - e^{-\frac{|\omega|}{2}(n+m)}\right), \hspace{10mm} & n \neq m, \\ 2 e^{-\frac{|\omega|}{2}} - e^{-|\omega| n} ~2\cosh \frac{\omega}{2}, & n = m. \end{array} \right. \end{equation*}Therefore, for \(n \neq m\), we get
\begin{equation*} \sum_{l=1}^\infty B_{nl} (\omega) \left[ \delta_{lm} + A_{lm} (\omega)\right] = A_{nm} (\omega) - A_{nm}(\omega) - B_{nm} (\omega) = -B_{nm} (\omega) \end{equation*}whereas for \(n = m\) we obtain (using \(A_{nn} (\omega) = \coth \frac{|\omega|}{2} \left( 1 - e^{-|\omega| n} \right)\))
\begin{equation*} \sum_{l=1}^\infty B_{nl} (\omega) \left[ \delta_{ln} + A_{ln} (\omega)\right] =\frac{1}{\sinh \frac{|\omega|}{2}} \left( (1 - e^{-|\omega| n}) \cosh \frac{\omega}{2} - e^{-\frac{|\omega|}{2}} + e^{-|\omega| n} ~\cosh \frac{\omega}{2} \right) = 1. \end{equation*}We moreover have the identity
<<h.ba>>
To obtain a simpler form of the TBA equations, let us start by rewriting the equilibrium conditions h.tba1 as
\begin{equation*} \ln (1 + \eta_n (\lambda)) - \sum_{m=1}^\infty \left[ \delta_{nm} + A_{nm} \right] * \ln (1 + \eta_m^{-1} (\lambda)) = \frac{h n - \pi J a_n (\lambda)}{T}. \end{equation*}Convolving this with \(\sum B\), using
\begin{equation*} \sum_{m=1}^\infty B_{nm} * m = \sum_m m \int_{-\infty}^\infty d\lambda B_{nm} (\lambda) = \sum_m m B_{nm} (\omega = 0) = 0 \end{equation*}and the identities h.b1 and h.ba, we obtain the simple system
<<h.tbaf>>
Amazingly, the magnetic field does not appear in this infinite set of coupled equations. In fact, we must at this stage recognize that the system we have obtained in h.tbaf is incomplete as it stands. Namely, the functions \(\eta_n\) for large \(n\) can take larger and larger values, and as such our sequence of equations is divergent, but the nature of this divergent is set by information not contained in h.tbaf. The asymptotics at large \(n\) are however easy to read from our original form of the TBA equations h.tba1: as \(n \rightarrow \infty\), \(\eta_n \rightarrow \infty\) in such a way that
<<h.tbaa>>
Setting this asymptotic condition renders the solution of h.tbaf unique.
An equivalent rewriting of these equations makes use of the definitions
\begin{equation*} \eta_n (\lambda) \equiv e^{\varepsilon_n(\lambda)/T} \end{equation*}to obtain
<<h.tbae>>
Determining the densities
To determine the densities \(\rho_n(\lambda)\) and \(\rho_n^h(\lambda)\), one can for example proceed as follows. The \(\eta_n\) are functions of \(\lambda\) and implicitly of \(J, h\) and \(T\). From h.tba1, one gets for example the derivative system
<<h.tbafd>>
By inspection, at the hand of l.bec, on finds that
<<h.tbafr>>
To find the densities, one can thus start by solving the factorized system h.tbaf (using the associated asymptotic conditions h.tbaa for the \(\eta_n\). Thereafter a solution can be found to h.tbafd, and substituted in h.tbafr.
Limiting cases
High-temperature limit
At high temperatues, the driving term is the equation for \(\eta_1\) becomes negligible, and the become independent of rapidity. The coupled system of equations simplifies to
\begin{equation*} \eta_1^2 = 1 + \eta_2, \hspace{5mm} \eta_n^2 = (1 + \eta_{n-1}) (1 + \eta_{n+1}) \hspace{3mm} (n > 1), \hspace{5mm} \lim_{n\rightarrow \infty} \frac{\ln \eta_n}{n} = \frac{h}{T}. \end{equation*}This second-order difference system has the following solution:
\begin{equation*} \eta_n = \left( \frac{\sinh(\frac{h}{2T}(n+1))}{\sinh(\frac{h}{2T})} \right)^2 - 1. \end{equation*}Low-temperature limit
We start by rewriting h.tba1 as
\begin{equation*} \ln (1 + e^{\varepsilon_n (\lambda)/T}) = hn - \pi J a_n (\lambda) + \sum_{m=1}^\infty \left( \delta_{nm} + A_{nm}\right) * \ln (1 + e^{-\varepsilon_m (\lambda)/T}). \end{equation*}As can be seen from the equilibrium conditions (most easily from h.tbaf), all functions \(\varepsilon_n\) with \(n > 1\) are positive-valued for any \(\lambda\), leaving \(\varepsilon_1\) as the only function which suffers a sign change. Considering the \(T \rightarrow 0^+\) limit and writing the positive(resp. negative)-valued parts of \(\varepsilon_1\) as \(\varepsilon_1^{(+)}\) (resp. \(\varepsilon_1^{(-)}\)), we obtain
\begin{equation*} \varepsilon_n (\lambda) = hn - \pi J a_n (\lambda) - A_{n1} * \varepsilon_1^{(-)} (\lambda), \hspace{5mm} n > 1 \end{equation*}for all \(n > 1\) functions, which are fully determined once we solve
\begin{equation*} \varepsilon_1^{(+)} (\lambda) + (1 + A_{11}) * \varepsilon_1^{(-)} (\lambda) = h - \pi J a_1 (\lambda). \end{equation*}Performing a Fourier transformation, [TBC]
The Algebraic Bethe Ansatz
General considerations and the Yang-Baxter equation
Let us start from the naive definition of quantum integrability, namely: \({\bf QI:N}\) A system is quantum integrable if:
- there is a complete set of quantum operators \(\hat{\boldsymbol Q} = (\hat{Q}_1, \hat{Q}_2, ...)\) which are constants of motion (conserved charges), \(\left[ \hat{H}, \hat{\boldsymbol Q} \right] = 0\).
- all conserved charges are in involution (commute with each other), \(\left[ \hat{Q}_n, \hat{Q}_m \right] = 0 ~~ \forall n, m\).
Let us use this as inspiration, and try to construct integrable models from scratch. First of all, we'd like to do the whole job in one go. Instead of constructing the charges one by one, we'd thus like to construct a generating function for them. Let's define a function \(\tau\) (which we'll end up calling the transfer matrix), taking operator values in the Hilbert space and taking as argument a spectral parameter \(\lambda\):
<<tau>>
(in which \(i_n\) are arbitrary numerical constants). Then,
<<Qn>>
The statement that all conserved charges are in involution then becomes equivalent to the statement that the transfer matrix commutes for all values of the spectral parameter,
<<tauc>>
The central idea of the Algebraic Bethe Ansatz is to provide a formalism for generating such commuting transfer matrices.
To find representations of tauc, we can proceed as follows. First, we introduce the notion of an auxiliary space: that is, we let the transfer matrix be the trace over a space \({\cal A}\) of a new object \(T(\lambda)\) which we'll call the monodromy matrix:
<<tautrT>>
The auxiliary space is any space we want. For simplicity, we start here by taking it to be a two-dimensional vector space isomorphic to \(\mathbb{C}^2\). The monodromy matrix therefore acts in the tensor product space \({\cal A} \otimes {\cal H}\) of auxiliary and Hilbert spaces.
Condition tauc is fulfilled provided
\begin{equation*} \left[ (\mbox{Tr}_{{\cal A}} T(\lambda)), (\mbox{Tr}_{{\cal A}} T(\mu)) \right] = 0. \end{equation*}Let's now consider the tensor product of two separate auxiliary spaces \({\cal A}_{1,2}\) (the tensored auxiliary space). Define the operators \(T_{1,2}(\lambda)\) acting in \({\cal A}_1 \otimes {\cal A}_2 \otimes {\cal H}\) as
\begin{equation*} T_1 (\lambda) = T(\lambda) \otimes {\bf 1}_2, \hspace{1cm} T_2 (\lambda) = {\bf 1}_1 \otimes T(\lambda). \end{equation*}Since the product of traces in a tensor product is the trace in the tensor product space, we have
<<trT1T20>>
or in other words
<<trT1T2c>>
(this relation, since we have taken the trace in both auxiliary spaces, is now really a commutation relation in Hilbert space).
The cyclic property of the trace in tensored auxiliary space and the property trT1T2c means that the products \(T_1 T_2\) and \(T_2 T_1\) must be related by a similarity transformation \(R_{12} (\lambda, \mu) \in {\cal A}_1 \otimes {\cal A}_2\) (the subindices indicate in which spaces the \(R\) matrix acts), in other words we can solve trT1T20 by requiring that \(T_1\) and \(T_2\) are intertwined by an invertible \(R\)-matrix,
\begin{equation*} R_{12} (\lambda, \mu) T_1 (\lambda) T_2 (\mu) (R_{12}(\lambda,\mu))^{-1} = T_2 (\mu) T_1 (\lambda) \end{equation*}or in other words
<<RTTeTTR>>
Finding a representation of this relation (i.e. finding an \(R\) matrix and a monodromy matrix associated to it) thus constitutes the key to defining a set of commuting quantum operators, and therefore a class of \({\bf QI:N}\) integrable models.
We can investigate the restrictions on possible \(R\) matrices. First of all, any \(R\) matrix must be nonsigular,
\begin{equation*} \mbox{Det} ~R_{12} (\lambda,\mu) \neq 0, \end{equation*}except at isolated points of \(\lambda,\mu\), which guarantees the existence of an inverse (which is both a left- and right-inverse since \(R\) is square by construction). Second, applying the permutation operator \(P_{12}\) (such that \(P_{12} M_{12} P_{12} = M_{21}\) for any matrix \(M\) in \({\cal A}_1 \otimes {\cal A}_2\)) in RTTeTTR leads to
\begin{equation*} (R_{21} (\mu,\lambda))^{-1} T_1 (\lambda) T_2 (\mu) = T_2 (\mu) T_1 (\lambda) (R_{21} (\mu,\lambda))^{-1}. \end{equation*}We must thus have
\begin{equation*} R_{12} (\lambda,\mu) = f(\lambda,\mu) (R_{21}(\mu,\lambda))^{-1} \end{equation*}where \(f(\lambda,\mu)\) is a \(\mathbb{C}\)-valued function. Since \(R_{12}(\lambda,\mu)\) is invertible from the left or right, we have that \(f(\lambda,\mu) = f(\mu,\lambda)\) and \(\left[R_{12} (\lambda,\mu), R_{21} (\mu,\lambda) \right] = 0\). We can rescale \(R\) by an arbitrary scaling function without modifying RTTeTTR, and therefore can without loss of generality impose the constraint
<<RRe1>>
A further important constraint on possible \(R\) matrices comes from the compatibility conditions for RTTeTTR. Namely, if we were to consider the triple tensor product of auxiliary spaces and define \(T_1\), \(T_2\) and \(T_3\), we can change the product \(T_1(\lambda) T_2 (\mu) T_3 (\nu)\) to \(T_3(\nu) T_2(\mu) T_1(\lambda)\) in two different ways; a sufficient (but not necessary) condition for the result to be identical is for the \(R\) matrix to obey the Yang-Baxter relation
<<YB>>
This automatically guarantees that all higher products are also consistently defined.
Note that in this whole story, we haven't mentioned anything about dimensionality of the physical space in which we'd like our model to live. This restriction will come later, as a convenience to define local Hamiltonian densities.
Constructing \(R\) matrices
Let us now attempt to construct explicit \(R\) matrices fulfilling the inversion requirement RRe1 and the Yang-Baxter relation YB. We proceed as systematically as possible. We begin by the simplest nontrivial auxiliary space we can consider, \({\cal A} \sim \mathbb{C}^2\). The smallest interesting \(R\) matrices are thus represented as \(4 \times 4\) matrices,
\begin{equation*} R(\lambda,\mu) = \left( \begin{array}{cccc} r_{11}(\lambda,\mu) & r_{12}(\lambda,\mu) & r_{13}(\lambda,\mu) & r_{14}(\lambda,\mu) \\ r_{21}(\lambda,\mu) & r_{22}(\lambda,\mu) & r_{23}(\lambda,\mu) & r_{24}(\lambda,\mu) \\ r_{31}(\lambda,\mu) & r_{32}(\lambda,\mu) & r_{33}(\lambda,\mu) & r_{34}(\lambda,\mu) \\ r_{41}(\lambda,\mu) & r_{42}(\lambda,\mu) & r_{43}(\lambda,\mu) & r_{44}(\lambda,\mu) \end{array} \right) \end{equation*}For the monodromy matrix, we can write the representation
<<TeABCD>>
in which \(A, B, C, D\) are operators in the (as yet unspecified) Hilbert space. Using natural tensor conventions
\begin{equation*} M \otimes N = \left(\begin{array}{cccc} M_{11} N_{11} & M_{11} N_{12} & M_{12} N_{11} & M_{12} N_{12} \\ M_{11} N_{21} & M_{11} N_{22} & M_{12} N_{21} & M_{12} N_{22} \\ M_{21} N_{11} & M_{21} N_{12} & M_{22} N_{11} & M_{22} N_{12} \\ M_{21} N_{21} & M_{21} N_{22} & M_{22} N_{21} & M_{22} N_{22} \end{array} \right) \end{equation*}we have (for the purposes of RTTeTTR)
\begin{equation*} T_1 (\lambda) = \left( \begin{array}{cccc} A(\lambda) & 0 & B(\lambda) & 0 \\ 0 & A(\lambda) & 0 & B(\lambda) \\ C(\lambda) & 0 & D (\lambda) & 0 \\ 0 & C(\lambda) & 0 & D(\lambda) \end{array} \right) \hspace{1cm} T_2 (\mu) = \left( \begin{array}{cccc} A (\mu) & B(\mu) & 0 & 0 \\ C (\mu) & D(\mu) & 0 & 0 \\ 0 & 0 & A (\mu) & B(\mu) \\ 0 & 0 & C (\mu) & D(\mu) \end{array} \right) \end{equation*} \begin{equation*} T_1 (\lambda) T_2 (\mu) = \left( \begin{array}{cccc} A(\lambda) A(\mu) & A(\lambda) B(\mu) & B(\lambda) A(\mu) & B(\lambda) B(\mu) \\ A(\lambda) C(\mu) & A(\lambda) D(\mu) & B(\lambda) C(\mu) & B(\lambda) D(\mu) \\ C(\lambda) A(\mu) & C(\lambda) B(\mu) & D(\lambda) A(\mu) & D(\lambda) B(\mu) \\ C(\lambda) C(\mu) & C(\lambda) D(\mu) & D(\lambda) C(\mu) & D(\lambda) D(\mu) \end{array} \right) \end{equation*} \begin{equation*} T_2 (\mu) T_1 (\lambda) = \left( \begin{array}{cccc} A(\mu) A(\lambda) & B(\mu) A(\lambda) & A(\mu) B(\lambda) & B(\mu) B(\lambda) \\ C(\mu) A(\lambda) & D(\mu) A(\lambda) & C(\mu) B(\lambda) & D(\mu) B(\lambda) \\ A(\mu) C(\lambda) & B(\mu) C(\lambda) & A(\mu) D(\lambda) & B(\mu) D(\lambda) \\ C(\mu) C(\lambda) & D(\mu) C(\lambda) & C(\mu) D(\lambda) & D(\mu) D(\lambda) \end{array} \right) \end{equation*}Choosing a form for the \(R\) matrix thus sets the form of the commutation relations between \(A, B, C, D\) operators. Once all entries of the \(R\) matrix are set, all these relations are also set. The logic we follow in this section is to first set the form of possible \(R\) matrices. For each form, we give the commutation relations of \(A, B, C, D\) operators.
Diagonal \(R\) matrices
The simplest form of \(R\) matrix we can begin with is a diagonal one,
\begin{equation*} ^{0}R (\lambda, \mu) = \left( \begin{array}{cccc} r_{11} (\lambda,\mu) & 0 & 0 & 0 \\ 0 & r_{22} (\lambda, \mu) & 0 & 0 \\ 0 & 0 & r_{33} (\lambda, \mu) & 0 \\ 0 & 0 & 0 & r_{44} (\lambda,\mu) \end{array} \right) \end{equation*}which trivially satisfies the Yang-Baxter relation for any functions \(r_{ii}\). Invariance under rescaling by an arbitrary function allows us to set \(r_{11} (\lambda,\mu) = 1\). The inversion relation RRe1 requires \(r_{22} (\lambda,\mu) r_{33} (\mu,\lambda) = 1\) and \(r_{44} (\lambda,\mu) r_{44} (\mu,\lambda) = 1\), so we write
\begin{equation*} r_{22} (\lambda,\mu) = e^{s (\lambda,\mu)}, \hspace{5mm} r_{33} (\lambda,\mu) = e^{-s(\lambda,\mu)}, \hspace{5mm} r_{44} (\lambda,\mu) = (-1)^\Theta e^{t (\lambda,\mu)}, \nonumber \\ s(\lambda,\mu) ~\mbox{arbitrary}, \hspace{1cm} t(\lambda,\mu) = -t(\mu,\lambda), \hspace{1cm} \Theta = 0,1. \end{equation*}The simplest nondiagonal form for an \(R\) matrix
The simplest \(R\)-matrix which can be defined above diagonal ones takes the generic form
<<R1>>
For calculations, it is convenient to represent this matrix as
<<R1r>>
In order for this to be a proper \(R\) matrix, we must impose the self-consistency requirements RRe1 and YB.
Constraint RRe1 yields the conditions
<<bc12>>
while the Yang-Baxter relation YB leads to
<<bc345>>
Operator algebra
Now that the structure of our R-matrix is set, let's look more closely at our monodromy matrix. We want to get rid of auxiliary space altogether, and write all our algebraic relations in terms of operators in the Hilbert space. For the particular choice of R-matrix given by R1, we thus get
\begin{align*} R (\lambda, \mu) T_1 (\lambda) T_2 (\mu) = \left( \begin{array}{cc} A(\lambda) A(\mu) & A(\lambda) B(\mu) \\ b(\lambda, \mu) A(\lambda) C(\mu) + c(\lambda, \mu) C(\lambda) A(\mu) & b(\lambda, \mu) A(\lambda) D(\mu) + c(\lambda, \mu) C(\lambda) B(\mu) \\ c(\lambda, \mu) A(\lambda) C(\mu) + b(\lambda, \mu) C(\lambda) A(\mu) & c(\lambda, \mu) A(\lambda) D(\mu) + b(\lambda, \mu) C(\lambda) B(\mu) \\ C(\lambda) C(\mu) & C(\lambda) D(\mu) \end{array} \right. \hspace{1mm}\nonumber\\ \left. \begin{array}{cc} B(\lambda) A(\mu) & B(\lambda) B(\mu) \\ b(\lambda, \mu) B(\lambda) C(\mu) + c(\lambda,\mu) D(\lambda) A(\mu) & b (\lambda, \mu) B(\lambda) D(\mu) + c(\lambda, \mu) D(\lambda) B(\mu) \\ c(\lambda, \mu) B(\lambda) C(\mu) + b(\lambda,\mu) D(\lambda) A(\mu) & c(\lambda, \mu) B(\lambda) D(\mu) + b(\lambda, \mu) D(\lambda) B(\mu) \\ D(\lambda) C(\mu) & D(\lambda) D(\mu) \end{array} \right) \end{align*}and
\begin{align*} T_2(\mu) T_1(\lambda) R (\lambda, \mu) = \left( \begin{array}{cc} A(\mu) A(\lambda) & b(\lambda, \mu) B(\mu) A(\lambda) + c(\lambda,\mu) A(\mu) B(\lambda) \\ C(\mu) A(\lambda) & b(\lambda, \mu) D(\mu) A(\lambda) + c(\lambda,\mu) C(\mu) B(\lambda) \\ A(\mu) C(\lambda) & b(\lambda, \mu) B(\mu) C(\lambda) + c(\lambda,\mu) A(\mu) D(\lambda) \\ C(\mu) C(\lambda) & b(\lambda, \mu) D(\mu) C(\lambda) + c(\lambda,\mu) C(\mu) D(\lambda) \end{array} \right. \hspace{1mm}\nonumber\\ \left. \begin{array}{cc} c(\lambda, \mu) B(\mu) A(\lambda) + b(\lambda,\mu) A(\mu) B(\lambda) & B(\mu) B(\lambda) \\ c(\lambda, \mu) D(\mu) A(\lambda) + b(\lambda,\mu) C(\mu) B(\lambda) & D(\mu) B(\lambda) \\ c(\lambda, \mu) B(\mu) C(\lambda) + b(\lambda,\mu) A(\mu) D(\lambda) & B(\mu) D(\lambda) \\ c(\lambda, \mu) D(\mu) C(\lambda) + b(\lambda,\mu) C(\mu) D(\lambda) & D(\mu) D(\lambda) \end{array} \right) \end{align*}This represents a set of nontrivial commutation/product relations between the \(A,B,C,D\) operator functions (for practical reasons, these are often written such that the order of the two operators is changed from one side of the equality to the other):
<<ABCDcr>>
(in which the notation \((ab)\) to the left of each equation means we have used the \(a,b\) matrix element directly, and \((\bar{cd})\) the \(cd\) one with \(\lambda \leftrightarrow \mu\)). Note that bc12 ensure that (\bar{13}) and (\bar{12}) are consistent with each other, and similarly for other pairs of equations.
For notational convenience, we define the following functions (pay attention to the order of the arguments)
<<fg>>
(note that \(g(\mu, \lambda) = -g(\lambda, \mu)\) due to bc12), which allows us to rewrite ABCDcr into the slightly shorter form
<<ABCDcrs>>
K.VII.1.11-24
Eigenstates of the transfer matrix
Remember that the monodromy matrix entries \(A(\lambda), B(\lambda), C(\lambda), D(\lambda)\) are taken to be functions taking operator values in some Hilbert space which we haven't specified yet. These obey commutation relations (a quadratic algebra) specified by ABCDcr, once the \(R\)-matrix is specified. We expect that these operator-valued functions are sufficient to navigate our whole Hilbert space, however we choose the latter to be defined. Let us try to develop some intuition of their meaning.
First of all, our generating function for conserved charges, the transfer matrix tau, takes from tautrT, TeABCD a simple form in terms of these operators:
<<tauAD>>
We are looking for states simultaneously diagonalizing all conserved charges: these are obtained automatically by seeking eigenstates of the transfer matrix itself, so we will be looking for eigenstates of \(A(\lambda) + D(\lambda)\). On the other hand, the form of the monodromy matrix TeABCD suggests to interpret \(B\) as a raising operator and \(C\) as a lowering operator within our Hilbert space.
To make a start building actual eigenstates, we assume the existence of a pseudovacuum \(|0\rangle\), which will be interpreted as the highest-weight state of the monodromy operators algebra. For definiteness, we also assume that it simultaneously diagonalizes the \(A\) and \(D\) operators summing up to transfer matrix, and that the lowering operator \(C\) annihilates it:
<<pv>>
where the functions \(a(\lambda)\) and \(d(\lambda)\) can be chosen arbitrarily.
The pseudovacuum is therefore by construction an eigenstate of the transfer matrix:
<<taupv>>
To construct further eigenstates of the transfer matrix, we consider applying our raising operator \(B\) repeatedly on the pseudovacuum. In generality, let us consider the state
<<prodBpv>>
for generic \(M\) and \(\{ \lambda_j \}_M\). Note the very important fact that the order in the product is immaterial, in view of the commutation relation ABCDcr \((14)\).
To check how the transfer matrix acts on such a state, we start by computing the action of \(A\). The result is
<<AprodBpv>>
The form of the action of this operator is easy to establish intuitively. When commuting \(A(\lambda)\) through a \(B(\lambda_j)\) using ABCDcr \((\bar{13})\), two types of terms are produced: one maintaining the function arguments, the other exchanging them. The only possible arguments of the \(M+1\) operators \(A, B\) are thus \(\lambda, \{ \lambda_j \}\). Assuming that all \(\lambda_j\) are distinct, once we have commuted \(A\) all the way through, if \(A\) has argument \(\lambda\), the first term with coefficient \(\lambda\) is obtained (and we have always used the first term on the right-hand side of ABCDcr \((\bar{13})\)). Otherwise if the argument \(\lambda\) is exchanged to an operator \(B\), the second term is obtained.
Similarly, we obtain the action of \(D\) on states prodBpv:
<<DprodBpv>>
A state prodBpv will thus be an eigenstate of the transfer matrix if \(\Lambda_j + \bar{\Lambda}_j = 0\), that is if
<<BER1>>
in which we have used bc12. These are the Bethe equations (constraints on the sets of rapidities \(\{ \lambda_j \}\)) guaranteeing that prodBpv are eigenstates of the transfer matrix tau
<<taue>>
with eigenvalues
<<tauev>>
For later convenience, we also mention here the action of the operator \(C\) on a state, which can be derived according to a logic very similar to that leading to AprodBpv and DprodBpv:
<<CprodBpv>>
where
<<LC>>
which again looks more compact using the notations fg
<<LCfg>>
Dual states
To define a measure in our Hilbert space, we also introduce the dual pseudovacuum \(\langle 0 | = | 0 \rangle^{\dagger}\), with properties
<<dpv>>
Similarly to states prodBpv, the dual states
<<dpvprodC>>
are eigenstates of the transfer matrix tau with eigenvalue tauev if the set \(\{ \lambda_j \}_M\) satisfies the Bethe equations BER1. This allows us to easily prove the orthogonality condition
<<lClBo>>
from the fact that
\begin{equation*} \langle \{ \lambda_j^C \}_M | \tau (\lambda) | \{ \lambda_k^B \}_M \rangle = \tau (\lambda | \{ \lambda_j^C \}_M) \langle \{ \lambda_j^C \}_M | \{ \lambda_k^B \}_M \rangle = \tau (\lambda | \{ \lambda_k^B \}_M ) \langle \{ \lambda_j^C \}_M | \{ \lambda_k^B \}_M \rangle \end{equation*}and that
\begin{equation*} \tau (\lambda | \{ \lambda_j^C \}_M) \neq \tau (\lambda | \{ \lambda_k^B \}_M ), ~~\{ \lambda_j^C \}_M \neq \{ \lambda_k^B \}_M. \end{equation*}We will consider the normalization of eigenstates explicitly later on, after proving an extremely important theorem due to N. A. Slavnov.
General comments
Formally, we have thus gone remarkably far without specifying much at all. Our simplest version of the \(R\)-matrix R1 still contains unspecified functions. We have not yet specified anything about our Hilbert space, except for assuming the existence of the highest-weight state/pseudovacuum pv. We have not yet defined our transfer matrix tau, besides assuming its existence. We have however in principle completely solved the eigenvalue problem for any specific choice we might make of all these objects. Defining an integrable model thus translates to finding a specific representation of the algebraic structures we have defined. This immense flexibility and power for generalization is the main strength of the Algebraic Bethe Ansatz.
Finding an explicit \(R\)-matrix of the simplest form
Let us begin by making a choice for the \(b,c\) functions in R1. The first observation is that we wish for rapidity-dependent operators (to make our model nontrivial), and we thus ignore the simple case of constant functions. To simplify things as much as possible, we also choose these two-parameter functions to be functions of a single parameter, and write (by an abuse of notation) \(b(\lambda,\mu) \equiv b(\lambda - \mu)\) and \(c(\lambda,\mu) \equiv c(\lambda - \mu)\).
We now suppose that \(b(\lambda)\) and \(c(\lambda)\) are analytic, and that they are bounded at \(|\lambda| \rightarrow \infty\). Starting with the off-diagonal function \(c\), we can put it to the simplest such non-constant function, namely a single pole
\begin{equation*} c(\lambda) \equiv \frac{c_0}{\lambda + \eta} \end{equation*}where \(c_0\) and \(\eta\) are finite generic complex constants. The constraint bc12 (left) means that \(b(\lambda)\) must like \(c(\lambda)\) have a single pole at \(\lambda = -\eta\), and that it must have the asymptotic value \(\lim_{\lambda \rightarrow \infty} b(\lambda) = 1\). We thus must use a form
\begin{equation*} b(\lambda) \equiv 1 + \frac{b_0}{\lambda + \eta}. \end{equation*}Equating the residues at the \(\lambda = -\eta\) pole in Equations bc12 then yield the constraints \(b_0 = -\eta\), \(c_0 = \eta\). Conditions bc345 are then also fulfilled. We thus obtain our first fully-fledged \(R\)-matrix, the "rational" matrix defined as
<<Rr>>
Note that we can write this as
<<R1P>>
where \(\mathbb{P}\) is the permutation matrix,
<<Pmat>>
Note that Rr can be related to an equivalent form commonly used in the literature:
<<Rru>>
The exact correspondence with Rr is
<<RRru>>
Constructing integrable models
Finding an explicit model associated to the simplest \(R\)-matrix
Let us now go further towards defining actual models using this logic. Now that the \(R\)-matrix is fully specified, all commutation relations ABCDcr are fixed. We have however not yet defined the transfer matrix tau or rather the monodromy matrix TeABCD besides these conditions on the \(A,B,C,D\) operators. Neither have we defined the Hilbert space itself.
Let us start by looking at constructing a monodromy matrix explicitly. We are thus looking for a representation of \(T\) in RTTeTTR. One obvious possible route comes from looking at YB: if we simply take the monodromy matrix to be constructed directly from the \(R\)-matrix, we will be able to satisfy RTTeTTR. The \(R\)-matrix we have defined is however a matrix in \({\cal A}\otimes{\cal A}\), where we have chosen the auxiliary space to be two-dimensional. This suggests to start from basic two-dimensional Hilbert spaces isomorphic to auxiliary space, \({\cal H}_j \sim {\cal A}\), for a set of labels \(j\).
Let us define a matrix \(L_j\) living in \({\cal A} \otimes {\cal H}_j\) as
<<LeR>>
where the subscript \(aj\) on the \(R\)-matrix means that the matrix acts in \({\cal A} \otimes {\cal H}_j\), and in which we have introduced parameters \(\xi_j\) called inhomogeneity parameters. We can then construct a nontrivial Hilbert space by tensoring these basic Hilbert spaces, \({\cal H} = \otimes_{j=1}^N {\cal H}_j\). We can then construct a monodromy matrix as
<<TprodL>>
This matrix obeys RTTeTTR by construction, in view of its construction as a product of \(R\)-matrices LeR and the Yang-Baxter relation YB.
We then have explicitly (using Rr and LeR in TprodL)
\begin{align*} T(\lambda) &= \left[b(\lambda - \xi_N) {\bf 1} + c(\lambda - \xi_N) \mathbb{P} \right]_{aN} \left[ b(\lambda - \xi_{N-1}) {\bf 1} + c(\lambda - \xi_{N-1}) \mathbb{P} \right]_{aN-1} ... \left[ ... \right]_{a1} \nonumber \\ &= (\lambda - \xi_N + \eta)^{-N} \left[ (\lambda - \xi_N) {\bf 1} + \eta \mathbb{P} \right]_{aN} \left[ ... \right]_{aN-1} ... \left[ ... \right]_{a1}. \end{align*}If we define without loss of generality the pseudovacuum \(| 0 \rangle\) as the vector \((1, 0, 0, ...)\), direct calculations show that this choice of monodromy matrix then imposes
<<adR1>>
Let us from now on put \(\xi_j = \xi ~\forall j\) (homogeneous limit) for simplicity, so \(d(\lambda) = b(\lambda - \xi)^N\). Evaluating the monodromy matrix at \(\lambda \rightarrow \xi\) gives
\begin{equation*} T (\xi) = \mathbb{P}_{aN} \mathbb{P}_{aN-1} ... \mathbb{P}_{a1} = \mathbb{P}_{a1} \mathbb{P}_{1N} \mathbb{P}_{1N-1} ... \mathbb{P}_{12} \end{equation*}where we have used the property \(\mathbb{P}_{ab} \mathbb{P}_{bc} = \mathbb{P}_{ac} \mathbb{P}_{ab}\) of the permutation operator to shift \(\mathbb{P}_{a1}\) from the right to the left. Taking the trace over auxiliary space, we get the transfer matrix evaluated at \(\lambda \rightarrow \xi\):
\begin{equation*} \tau (\xi) = \left(\mbox{Tr}_{\cal A} \mathbb{P}_{a1} \right) \mathbb{P}_{1N} \mathbb{P}_{1N-1} ... \mathbb{P}_{12} = \mathbb{P}_{1N} \mathbb{P}_{1N-1} ... \mathbb{P}_{12} \equiv U \end{equation*}(using \(\mbox{Tr}_{\cal A} \mathbb{P}_{aj} = {\bf 1}_j\)), where \(U\) is the cyclic shift operator. Since \(U^N = 1\), this operator has eigenvalues \(e^{ik}\) with \(k = \frac{2\pi}{N} n\), \(n \in \mathbb{Z}\). We thus construct our first integral of motion using Qn,
<<RrQ0>>
where \(P\) is the generator of translations, and thus is our momentum operator.
For the next integral of motion, we need
\begin{equation*} \frac{d}{d\lambda} \ln \tau (\lambda) |_{\lambda = \xi}. \end{equation*}We have the building block
\begin{equation*} \frac{d}{d\lambda} L_j (\lambda, \xi)|_{\lambda = \xi} = \frac{1}{\eta} \left[ {\bf 1} - \mathbb{P} \right]_{aj} \end{equation*}so
\begin{align*} \eta \frac{d}{d\lambda} \tau (\lambda) |_{\lambda = \xi} &= \mbox{Tr}_{\cal A} \left( \left[ {\bf 1} - \mathbb{P}\right]_{aN} \mathbb{P}_{aN-1} ... \mathbb{P}_{a1} + \mathbb{P}_{aN} \left[ {\bf 1} - \mathbb{P}\right]_{aN-1}\mathbb{P}_{aN-2} ... \mathbb{P}_{a1} + ... \right. \nonumber \\ &\hspace{5mm}\left. + \mathbb{P}_{aN} ... \mathbb{P}_{a3} \left[ {\bf 1} - \mathbb{P}\right]_{a2} \mathbb{P}_{a1} + \mathbb{P}_{aN} ... \mathbb{P}_{a2} \left[ {\bf 1} - \mathbb{P}\right]_{a1} \right) \nonumber \\ &= (\mbox{Tr}_{\cal A} \mathbb{P}_{a1}) \left( \left[ {\bf 1} - \mathbb{P}\right]_{1N} \mathbb{P}_{1N-1}...\mathbb{P}_{12} + \mathbb{P}_{1N} \left[ {\bf 1} - \mathbb{P}\right]_{1N-1} \mathbb{P}_{1N-2}...\mathbb{P}_{12} + ... \right. \nonumber \\ &\hspace{5mm}\left. + \mathbb{P}_{1N} ... \mathbb{P}_{13} \left[ {\bf 1} - \mathbb{P}\right]_{12} \right) + \mathbb{P}_{NN-1} \mathbb{P}_{NN-2} ... \mathbb{P}_{N2} \left[ {\bf 1} - \mathbb{P}\right]_{N1} (\mbox{Tr}_{\cal A} \mathbb{P}_{aN}) \end{align*}(in the second line, we have treated the last term slightly differently). Now because of tauc, we have \(\left[ \frac{d}{d\lambda} \tau(\lambda), \tau(\lambda') \right] = 0\), and therefore can write
\begin{equation*} \eta \frac{d}{d\lambda} \ln \tau (\lambda) |_{\lambda = \xi} = \eta ~\tau^{-1} (\lambda) \frac{d}{d\lambda} \tau(\lambda) |_{\lambda = \xi} = \sum_{j=1}^N \mathbb{P}_{j j+1} - {\bf 1}_{j j+1}. \end{equation*}Using the identity
<<sigsig2Pm1>>
we thus get
\begin{equation*} \eta \frac{d}{d\lambda} \ln \tau (\lambda) |_{\lambda = \xi} = \sum_{j=1}^N \frac{1}{2} \left[ \sigma_j \cdot \sigma_{j+1} - 1 \right] \end{equation*}so our second conserved charge is
<<RrQ1>>
We have thus derived the Heisenberg model from basic algebraic principles. Such an equation is called a trace identity: a conserved charge is obtained from taking derivatives of the generating function given, the latter being the log of the transfer matrix.
States of the form prodBpv diagonalize the transfer matrix (and thus all conserved charges simultaneously) provided the Bethe equations BER1 are satisfied for the functions Rr and adR1, i.e. if
\begin{equation*} \left[\frac{\lambda_j - \xi + \eta}{\lambda_j - \xi} \right]^N = \prod_{l (\neq j) = 1}^M \frac{\lambda_j - \lambda_k + \eta}{\lambda_j - \lambda_k - \eta} \end{equation*}(note however that we have not yet dealt with the important question of completeness). The eigenvalue of the transfer matrix on these states is
\begin{equation*} \tau (\lambda | \{ \lambda_j \}) = \prod_{j=1}^M \frac{\lambda_j - \lambda + \eta}{\lambda_j - \lambda} + \left[\frac{\lambda - \xi}{\lambda - \xi + \eta}\right]^N \prod_{j=1}^M \frac{\lambda_j - \lambda - \eta}{\lambda_j - \lambda}. \end{equation*}The eigenvalue equation for the momentum operator is thus
\begin{equation*} P | \{ \lambda_j \}_M \rangle = P (\{ \lambda_j \}) | \{ \lambda_j \}_M \rangle, \hspace{1cm} P (\{ \lambda_j \}) = -i \ln \tau(\xi | \{ \lambda_j \}) = -i \sum_{j=1}^M \ln \frac{\lambda_j - \xi + \eta}{\lambda_j - \xi}. \end{equation*}For the energy, we can similarly use the trace identity RrQ1 to get
\begin{equation*} E (\{ \lambda_j \}) = \frac{\eta}{2} \frac{d}{d\lambda} \ln \tau(\lambda | \{ \lambda_j \} )|_{\xi} = \frac{\eta^2}{2} \sum_{j=1}^M \frac{1}{(\lambda_j - \xi) (\lambda_j - \xi + \eta)}. \end{equation*}We have not yet specified the \(R\)-matrix parameter \(\eta\) or the inhomogeneity parameter \(\xi\). Our rapidity is until now an arbitrary parametrization whose scale and origin we can choose at will, so the value of \(\eta\) is immaterial (as long as it doesn't vanish, in which case our \(R\)-matrix would become trivial). On the other hand, we want our momentum and energy to be manifestly real. A convenient choice is thus to take
\begin{equation} \eta = i, \hspace{2cm} \xi = \eta/2 = i/2. \label{eq:etaxi} \end{equation}In the next section, we collect for convenience our final form for these equations.
General remarks
As we went along, we made a number of choices which simplified the construction. We can of course make these choices otherwise. One particularly important choice was to select the \(L\) operators such that they became the permutation matrix when evaluated at a specific value of the spectral parameter. This allowed us to extract the translation operator; the trace identities we used, involving the logarithm of a product of \(L\) operators, then ultimately led to conserved charges (e.g. the Hamiltonian) expressed in terms of a sum of (quasi-)local terms. This is physically reasonable, but in no way necessary to construct a Bethe Ansatz solvable model.
ABA for the isotropic \(S=1/2\) antiferromagnet (\(XXX\) model)
For convenience, we restate here all important formulas relevant for our further study of the isotropic \(XXX\) model, in the final parametrization which we have settled upon.
<<h.r>>
<<h.ad>>
<<h.te>>
<<h.q1>>
<<h.q1e>>
<<h.q2>>
<<h.q2e>>
A few overall comments are in order here. The form of the \(R\)-matrix we settled upon is not unitary. The construction we ended up with conforms to (some) historical conventions. This choice has as consequence that the monodromy matrix \(A,B,C,D\) operator entries are not simply related by the usual complex conjugation. This slight annoyance is of no consequence for our further purposes.
Another example: the trigonometric \(R\)-matrix and the anisotropic \(S=1/2\) antiferromagnet (\(XXZ\) model)
Another solution to the Yang-Baxter equation can be found, which has the same form as the rational \(R\)-matrix but slightly different matrix elements:
<<a.r>>
The logic of the Algebraic Bethe Ansatz can again be applied here, following the previous example of the \(XXX\) case. Adopting the same convention for the reference state (choosing also the homogeneous limit with \(\xi = \eta/2\), but leaving \(\eta\) here as a free parameter) yields
<<a.ad>>
The Bethe equations read
\begin{equation*} \left[\frac{\sinh(\lambda_j + \eta/2)}{\sinh (\lambda_j - \eta/2)} \right]^N = \prod_{k (\neq j) = 1}^M \frac{\sinh (\lambda_j - \lambda_k + \eta)}{\sinh(\lambda_j - \lambda_k - \eta)}. \end{equation*}The eigenvalue of the transfer matrix becomes
<<a.te>>
The first few conserved charges can be computed as
<<a.q1>>
giving eigenvalue
<<a.q1e>>
The Hamiltonian is (under an appropriate choice of the constant prefactor)
<<a.q2>>
in which \(\Delta = \cosh \eta\). The energy eigenvalue of a state is
<<a.q2e>>
For the gapped regime \(\Delta > 1\) we have that \(\eta\) is a real parameter. For the gapless regime \(0 < \Delta < 1\) it is convenient to reparametrize the anisotropy as \(\eta= -i\zeta\), so
<<da>>
Scalar products: Slavnov's formula
A crucial result by N. Slavnov concerns the scalar product of states constructed by the action of the operators \(B(\lambda)\) on the vacuum. Namely, we wish to compute
<<sp>>
in general, when at least one of the two sets \(\{ \mu \}\), \(\{ \lambda \}\) is solution to the Bethe equations. For definiteness, we consider \(\{ \lambda \}\) as such a set.
Slavnov's theorem 1989.Slavnov.TMP.79 then states that for \(\{ \lambda \}\) solution to the Bethe equations BER1 and for \(\{ \mu \}\) an arbitrary set of parameters, the scalar product \(S_M\) sp can be represented as a determinant,
<<ssp>>
where
\begin{equation*} T_{ab} = \frac{\partial}{\partial \lambda_a} \tau (\mu_b| \{ \lambda \}). %\hspace{0.3cm} V_{ab} = \frac{1}{\varphi(\mu_b - \lambda_a)}, \hspace{0.3cm} 1 \leq a, b \leq M. \end{equation*}Here,
\begin{equation*} \varphi (\lambda) \equiv \left\{ \begin{array}{cc} \lambda & \Delta = 1 \\ \sinh \lambda & |\Delta| < 1. \end{array} \right. \label{eq:phidef} \end{equation*}The proof of this is omitted here, and goes either through the direct use of the commutation relations between the operators to obtain recursion relations for the scalar products, or through Maillet's \(F\)-basis representation 1999.Kitanine.NPB.554.
In particular, specializing to the norm of Bethe eigenstates, a proof of Gaudin's norm formula is obtained through taking the limit \(\mu_a \rightarrow \lambda_a\), \(a=1, ..., M\):
<<gnf>>
with the Gaudin matrix entries being
<<gm>>
Matrix elements of physical operators
Solution of the quantum inverse problem
Until now, we have thus managed the first two steps needed to obtain correlation functions within the framework of the Algebraic Bethe Ansatz, namely: we can construct our eigenstates, and normalize them properly. However, the relationship between the operator entries of the monodromy matrix and local spin operators of the spin chain remains obscure at this stage. This problem is known as the quantum inverse problem, and we here present its solution.
The crucial remark is that, since \(b(0) = 0\) and \(c(0) = 1\), the \(L_n\) operator becomes a permutation matrix exchanging the auxiliary space with the \(n\)-th quantum space when the spectral parameter is put equal to the on-site inhomogeneity:
<<LasP>>
We consider the homogeneous case \(\xi_j = \xi\), \(j = 1, ..., N\) where things are slightly simpler. The monodromy matrix evaluated at \(\lambda = \xi\) takes the simple form
\begin{equation*} T(\xi) = P_{a N} P_{a N-1} ... P_{a 1} = P_{a 1} P_{1N} P_{1N-1} ... P_{12} = P_{a 1} U \end{equation*}where \(U = P_{1N} P_{1N-1} ... P_{12}\) is the cyclic shift operator in quantum space, and we have used \(P_{jk}P_{jl} = P_{kl}P_{jk}\). We can write this last equation in matrix form:
\begin{equation*} \left( \begin{array}{cc} A(\xi) & B(\xi) \\ C(\xi) & D(\xi) \end{array} \right) = \left( \begin{array}{cc} \frac{1 + \sigma^z_1}{2} & \sigma^-_1 \\ \sigma^+_1 & \frac{1- \sigma^z_1}{2} \end{array} \right) U \end{equation*}where \(\sigma^z_1\), \(\sigma^{\pm}_1 = \frac{\sigma^x_1 \pm i \sigma^y_1}{2}\) are the Pauli matrices associated to site \(1\). Solving for these gives
\begin{equation*} A(\xi) + D(\xi) = U, \hspace{0.3cm} A(\xi) - D(\xi) = \sigma^z_1 U, \nonumber \\ B(\xi) = \sigma^-_1 U, \hspace{1cm} C(\xi) = \sigma^+_1 U. \end{equation*}These are the required formulas for the first site. For the other sites, it's simply necessary to use the translation operator \(\sigma_j = U^{j-1} \sigma^a_1 U^{1 - j}\) and \(U^N = {\bf 1}\) to obtain the final formulas
\begin{align*} \sigma^z_j &= \left[ A(\xi) + D(\xi) \right]^{j-1} (A(\xi) - D(\xi)) \left[ A(\xi) + D(\xi) \right]^{N - j}, \nonumber \\ \sigma^-_j &= \left[ A(\xi) + D(\xi) \right]^{j-1} B(\xi) \left[ A(\xi) + D(\xi) \right]^{N - j}, \nonumber \\ \sigma^+_j &= \left[ A(\xi) + D(\xi) \right]^{j-1} C(\xi) \left[ A(\xi) + D(\xi) \right]^{N - j}. \end{align*}In the inhomogeneous case, a similar proof gives
<<sigABCD>>
This therefore provides the third ingredient needed for the computation of the correlation functions.
Determinant representation for matrix elements
We now compute the matrix elements of the local spin operators in the basis of Bethe eigenstates. Let's do the simplest example in some detail, the matrix element of the \(\sigma^-_j\) operator in the basis of the (as yet unnormalized) Bethe eigenstates:
\begin{equation*} F_j^- (\{ \mu \}_{M+1}, \{ \lambda \}_M) = \langle 0 | \prod_{k=1}^{M+1} C(\mu_k) ~\sigma^-_j \prod_{l=1}^M B(\lambda_l) | 0 \rangle. \end{equation*}Here, we consider that both sets \(\{ \mu \}_{M+1}\) and \(\{ \lambda \}_M\) are solution to Bethe equations. Using sigABCD, and the fact that Bethe eigenstates are eigenstates of the transfer matrix with eigenvalues
\begin{equation*} (A(\xi_j) + D(\xi_j)) \prod_{l=1}^M B(\lambda_l) | 0 \rangle = \prod_{k=1}^M b^{-1} (\lambda_k, \xi_j) \prod_{l=1}^M B(\lambda_l) | 0 \rangle, \end{equation*}we can therefore rewrite the matrix element as
\begin{align*} F_j^- (\{ \mu \}_{M+1}, \{ \lambda \}_M) &= \left[ \prod_{l=1}^{M+1} \prod_{k=1}^{j-1} b^{-1} (\mu_l, \xi_k)\right] \left[ \prod_{l=1}^{M} \prod_{k=j+1}^{N} b^{-1} (\lambda_l, \xi_k)\right] \langle 0 | \prod_{k=1}^{M+1} C(\mu_k) B(\xi_j) \prod_{l=1}^M B(\lambda_l) | 0 \rangle \nonumber \\ &= \phi_j^{-1} (\{ \lambda \}) \phi_{j-1} (\{ \mu \}) S_{M+1} (\{ \mu \}_{M+1}, \{ \xi_j, \{ \lambda \}_{M}) \end{align*}in which we have defined
\begin{equation*} \phi_j (\{ \lambda \}) = \prod_{l=1}^M \prod_{k=1}^j b^{-1} (\lambda_l, \xi_k) \end{equation*}and used the fact that \(\phi_N (\{ \lambda \}) = 1\), as can be seen from the Bethe equations.
Our job is done, since we can now make use of Slavnov's theorem ssp to obtain the scalar product \(S_{M+1}\) as a determinant. The final answer for the desired matrix element is then
<<sigminME>>
in which the \(H^{-}\) matrix entries are
<<Hmin>>
A similar but slightly longer calculation gives the matrix element for the \(\sigma^z\) operator,
<<sigzME>>
in which the \(H\) matrix entries are
<<sigzH>>
and \(P\) is a rank one matrix with entries
<<sigzP>>
Dynamical correlation functions
Sum rules
The f-sumrule
Consider a model with lattice sites \(j = 1, ..., N\). Let's look at the following generic correlation function of some operator \({\cal O}_j^a\), where \(a\) is some label (for example, for a lattice Bose gas, we could have \({\cal O}_j = \Psi_j\) or \(\Psi^\dagger_j\) or \(\rho_j \equiv \Psi_j^\dagger \Psi_j\)):
\begin{equation*} {\cal S}^{a \bar{a}} (k, \omega) \equiv \frac{1}{N} \sum_{j, j'} e^{-i k(j-j')} \int_{-\infty}^\infty dt e^{i\omega t} \langle \frac{1}{2} \left[ {\cal O}^a_j (t), ({\cal O}^a_{j'} (0))^\dagger \right] \rangle \end{equation*}The expectation value \(\langle ... \rangle\) can be any expectation value: with respect to a specific state, \(\langle ... \rangle = \langle \alpha | ... | \alpha \rangle\), a thermal average \(\langle ... \rangle = \frac{1}{\cal Z} \sum_{\gamma} \langle \gamma | ... | \gamma \rangle e^{-\beta (E_{\gamma} - \mu N_{\gamma})}\), it doesn't matter. In the case of a (grand-canonical) thermal average, we can write
\begin{equation*} {\cal S}^{a \bar{a}} (k, \omega) \equiv \frac{1}{N} \sum_{j, j'} e^{-i k(j-j')} \int_{-\infty}^\infty dt e^{i\omega t} \frac{1}{\cal Z} \sum_\gamma \langle \gamma | \frac{1}{2} \left[ {\cal O}^a_j (t), ({\cal O}^a_{j'} (0))^\dagger \right] | \gamma \rangle e^{-\beta (E_\gamma - \mu N_\gamma)} \end{equation*}in which \(\mu\) is the chemical potential, \({\cal Z}\) is the grand-canonical partition function, and \(\sum_{\gamma}\) represents a sum over eigenstates.
Consider integrating this correlation over all frequencies, calculating the first moment in frequency
\begin{equation*} I_k^{(1)} \equiv \int_{-\infty}^\infty \frac{d\omega}{2\pi} \omega ~{\cal S}^{a \bar{a}} (k, \omega) \end{equation*}This can be manipulated as follows:
\begin{align*} I_k^{(1)} &=& \frac{1}{2N} \int_{-\infty}^\infty \frac{d\omega}{2\pi} \omega \int_{-\infty}^\infty dt e^{i\omega t} \frac{1}{\cal Z} \sum_\gamma \langle \gamma | \left[ {\cal O}^a_k (t), ({\cal O}^a_{k'} (0))^\dagger \right] | \gamma \rangle e^{-\beta (E_\gamma - \mu N_\gamma)} \nonumber \\ &=& \frac{1}{2N} \int_{-\infty}^\infty \frac{d\omega}{2\pi} \omega \int_{-\infty}^\infty dt e^{i\omega t} \frac{1}{\cal Z} \times \nonumber \\ &&\times \sum_\gamma \sum_{\alpha} \left\{ e^{-i\omega_{\alpha \gamma}t} \langle \gamma | {\cal O}^a_k | \alpha \rangle \langle \alpha | ({\cal O}^a_k)^\dagger | \gamma \rangle - e^{i\omega_{\alpha \gamma}t} \langle \gamma | ({\cal O}^a_k)^\dagger | \alpha \rangle \langle \alpha | {\cal O}^a_k | \gamma \rangle \right\} e^{-\beta (E_\gamma - \mu N_\gamma)} \end{align*}in which we have used the Fourier transforms
\begin{equation*} {\cal O}^a_j = \frac{1}{N} \sum_k e^{ikj} {\cal O}^a_k, \hspace{5mm} {\cal O}^a_k = \sum_j e^{-ikj} {\cal O}^a_j \end{equation*}and have inserted a resolution of the identity \({\bf 1} = \sum_{\alpha} | \alpha \rangle \langle \alpha |\) in terms of eigenstates of the Hamiltonian. We have used the notation \(\omega_{\alpha \gamma} \equiv E_\alpha - E_\gamma - \mu(N_\alpha - N_\gamma)\), and the Heisenberg relation \({\cal O} (t) = e^{i (H - \mu N) t} {\cal O} e^{-i (H - \mu N)t}\) to resolve the time dependence.
Using the identity
\begin{equation*} \int_{-\infty}^\infty dt e^{i (\omega - \omega') t} = 2\pi \delta (\omega - \omega'), \end{equation*}we get
\begin{align*} I_k^{(1)} &= \frac{1}{2N} \int_{-\infty}^\infty d\omega \omega \frac{1}{\cal Z} \sum_\gamma \sum_\alpha \left\{ \delta (\omega - \omega_{\alpha \gamma}) \langle \gamma | {\cal O}^a_k | \alpha \rangle \langle \alpha | ({\cal O}^a_k)^\dagger | \gamma \rangle \right. \nonumber \\ & \left. \hspace{4cm}- \delta (\omega + \omega_{\alpha \gamma}) \langle \gamma | ({\cal O}^a_k)^\dagger | \alpha \rangle \langle \alpha | {\cal O}^a_k | \gamma \rangle \right\} e^{-\beta (E_\gamma - \mu N_\gamma)} \nonumber \\ &= \frac{1}{2N} \frac{1}{\cal Z} \sum_\gamma \sum_\alpha \omega_{\alpha \gamma} \left\{ \langle \gamma | {\cal O}^a_k | \alpha \rangle \langle \alpha | ({\cal O}^a_k)^\dagger | \gamma \rangle + \langle \gamma | ({\cal O}^a_k)^\dagger | \alpha \rangle \langle \alpha | {\cal O}^a_k | \gamma \rangle \right\} e^{-\beta (E_\gamma - \mu N_\gamma)} \nonumber \\ &= \frac{1}{2N} \frac{1}{\cal Z} \sum_\gamma \sum_\alpha \left\{ \langle \gamma | \left[ {\cal O}^a_k, H \right] | \alpha \rangle \langle \alpha | ({\cal O}^a_k)^\dagger | \gamma \rangle + \langle \gamma | ({\cal O}^a_k)^\dagger | \alpha \rangle \langle \alpha | \left[ H, {\cal O}^a_k \right] | \gamma \rangle \right\} e^{-\beta (E_\gamma - \mu N_\gamma)} \nonumber \\ &= \frac{-1}{2N} \frac{1}{\cal Z} \sum_\gamma \langle \gamma | \left[ \left[ H, {\cal O}^a_k \right], ({\cal O}^a_k)^\dagger \right] | \gamma \rangle e^{-\beta (E_\gamma - \mu N_\gamma)} \nonumber \\ &= \frac{-1}{2N} \langle \left[ \left[ H, {\cal O}^a_k \right], ({\cal O}^a_k)^\dagger \right] \rangle_\beta \end{align*}in which we have used the fact that we're working in a basis of energy eigenstates (so \(H | \alpha \rangle = (E_\alpha - \mu N_\alpha) | \alpha \rangle\)) and the resolution of the identity \(\sum_\alpha | \alpha \rangle \langle \alpha | = {\bf 1}\).
We thus get
\begin{equation*} \int_{-\infty}^\infty \frac{d\omega}{2\pi} \omega ~{\cal S}^{a \bar{a}} (k, \omega) = \frac{-1}{2N} \langle \left[ \left[ H, {\cal O}^a_k \right], ({\cal O}^a_k)^\dagger \right] \rangle \end{equation*}(note: this holds irrespective of how the average \(\langle ... \rangle\) is defined, provided \(S(k,\omega)\) and the right-hand side of this equation are averaged in precisely the same way). This relation holds for any correlator of any model.
Now: the magic trick comes from the fact that for specific cases, the right-hand side can be calculated exactly.
Lieb-Liniger
Let's consider the Lieb-Liniger model,
\begin{equation*} H_{LL} = \int_0^L dx \left\{ \Psi^\dagger (x) (-\partial_x^2) \Psi(x) + c \Psi^\dagger(x) \Psi^\dagger(x) \Psi(x) \Psi(x) - \mu \Psi^\dagger(x) \Psi(x) \right\} \end{equation*}with canonical equal-time commutation relations \(\left[ \Psi(x), \Psi^\dagger (x') \right] = \delta(x-x')\).
Notations used here: system length is \(L\), number of particles is \(N = \int_0^L dx \Psi^\dagger (x) \Psi(x)\) (previously, the integer \(N\) was the number of sites, which now gets replaced by the system length given by the continuous parameter \(L\); don't confuse these for each other).
We define the Fourier transforms as
\begin{equation*} \Psi (x) = \frac{1}{L} \sum_k e^{ikx} \Psi_k, \hspace{10mm} \Psi_k = \int_0^L dx e^{-ikx} \Psi (x) \end{equation*}so \(\left[ \Psi_k, \Psi^\dagger_{k'} \right] = L \delta_{k k'}\) and the Hamiltonian is
\begin{equation*} H_{LL} = \frac{1}{L} \sum_k (k^2 - \mu) \Psi^\dagger_k \Psi_k + \frac{c}{L^3} \sum_{k_1 k_2 q} \Psi^\dagger_{k_1 + q} \Psi^{\dagger}_{k_2 - q} \Psi_{k_2} \Psi_{k_1}. \end{equation*}Density-density correlations (dynamical structure factor)
The dynamical structure factor in our notations is then
\begin{equation*} {\cal S}^{\rho \rho} (k, \omega) = \frac{1}{L} \int_0^L dx dx' e^{-ik (x - x')} \int_{-\infty}^\infty dt e^{i\omega t} \langle \frac{1}{2}\left[ \rho(x,t), \rho(x',0) \right] \rangle \end{equation*}For the density operator, we write
\begin{equation*} \rho_k \equiv \int_0^L dx e^{-ikx} \rho(x) = \int_0^L dx e^{-ikx} \Psi^\dagger (x) \Psi(x) = \frac{1}{L} \sum_{k_1} \Psi^\dagger_{k_1} \Psi_{k_1 + k}. \end{equation*}For the f-sumrule applied to the dynamical structure factor, we get
\begin{equation*} \int_{-\infty}^\infty \frac{d\omega}{2\pi} \omega ~{\cal S}^{\rho \rho} (k, \omega) = \frac{-1}{2L} \langle \left[ \left[ H, \rho_k \right], \rho_{-k} \right] \rangle. \end{equation*}Let's calculate the right-hand side of the f-sumrule. Start with
\begin{equation*} \left[ H, \rho_k \right] = \frac{1}{L} \sum_{k_1} \left\{ \frac{1}{L} \sum_{k_2} (k_2^2 -\mu) \left[ \Psi^\dagger_{k_2} \Psi_{k_2}, \Psi^\dagger_{k_1} \Psi_{k_1 + k} \right] + \frac{c}{L^3} \sum_{k_3 k_4 q} \left[ \Psi^\dagger_{k_3 + q} \Psi^\dagger_{k_4 - q} \Psi_{k_4} \Psi_{k_3}, \Psi^\dagger_{k_1} \Psi_{k_1 + k} \right] \right\} \end{equation*}The commutator in the first term is
\begin{equation*} \Psi^\dagger_{k_2} \Psi_{k_1 + k} L \delta_{k_1 k_2} - \Psi^\dagger_{k_1} \Psi_{k_2} L \delta_{k_2, k_1 + k} \end{equation*}so the first term becomes
\begin{align*} \frac{1}{L} &\sum_{k_2} (k_2^2 - \mu) \left( \Psi^\dagger_{k_2} \Psi_{k_2 + k} - \Psi^\dagger_{k_2 - k} \Psi_{k_2} \right) \nonumber \\ &= \frac{1}{L} \sum_{k_2} (k_2^2 - (k_2 + k)^2) \Psi^\dagger_{k_2} \Psi_{k_2 + k} \nonumber \\ &= \frac{1}{L} \sum_{k_1} (-k)(k+2k_1) \Psi^\dagger_{k_1} \Psi_{k_1 + k}. \end{align*}The commutator in the second term is
\begin{equation*} \Psi^\dagger_{k_1} \left[ \Psi^\dagger_{k_3 + q} \Psi^\dagger_{k_4 - q}, \Psi_{k_1 + k} \right] \Psi_{k_4} \Psi_{k_3} + \Psi^\dagger_{k_3 + q} \Psi^\dagger_{k_4 - q} \left[ \Psi_{k_4} \Psi_{k_3}, \Psi^\dagger_{k_1} \right] \Psi_{k_1 + k} \end{equation*}Calculating this and performing the sums over \(k_1\), \(k_3\) and \(k_4\) shows that this whole second term vanishes. We thus get
\begin{equation*} \left[ H, \rho_k \right] = \frac{1}{L} \sum_{k_1} (-k)(k+2k_1) \Psi^\dagger_{k_1} \Psi_{k_1 + k}. \end{equation*}Going further (using \((\rho_k)^\dagger = \rho_{-k}\)),
\begin{align*} \left[ \left[ H, \rho_k \right], \rho_{-k} \right] &= \frac{1}{L^2} \sum_{k_1} (-k)(k+2k_1) \sum_{k_2} \left[ \Psi^\dagger_{k_1} \Psi_{k_1 + k}, \Psi^\dagger_{k_2} \Psi_{k_2 - k} \right] \nonumber \\ &= \frac{1}{L} \sum_{k_1} (-k) (k + 2k_1) \left( \Psi^\dagger_{k_1} \Psi_{k_1} - \Psi^\dagger_{k_1 + k} \Psi_{k_1 + k} \right) \nonumber \\ &= \frac{1}{L} \sum_{k_1} (-k)[k + 2k_1 - (-k + 2k_1)] \Psi^\dagger_{k_1} \Psi_{k_1} \nonumber \\ &= -2k^2 \frac{1}{L} \sum_{k_1} \Psi^\dagger_{k_1} \Psi_{k_1} = -2N k^2 \end{align*}We thus obtain the explicit f-sumrule for the dynamical structure factor,
<<l.dsf.fsr>>
This allows to check the overall intensity for fixed values of \(k\).
Lieb-Liniger
Spin-\(1/2\) chains
Integrability out of equilibrium
The Quench Action
Formalism
Interaction quench in Lieb-Liniger
Anisotropy quench in \(XXZ\)
Literature
Books
b-Gaudin
- Gaudin, La fonction d'onde de Bethe, Masson (Paris), 1983.
Russian translation:
English translation: M. Gaudin, The Bethe Wavefunction (translation by J.-S. Caux), Cambridge University Press, 2014.
@Book{Gaudin,
author = {M. Gaudin},
title = {La fonction d'onde de {B}ethe},
publisher = {Masson, Paris},
year = {1983},
note = {{\it The Bethe Wavefunction} (translation by J.-S. Caux), Cambridge University Press, 2014.},
}b-KBI
-
- Korepin and N. M. Bogoliubov and A. G. Izergin,
Quantum Inverse Scattering Method and Correlation Functions, Cambridge Univ. Press (1993).
@Book{KorepinBOOK,
author = {V. E. Korepin and N. M. Bogoliubov and A. G. Izergin},
title = {Quantum Inverse Scattering Method and Correlation Functions},
publisher = {Cambridge Univ. Press},
year = {1993}
}Articles
1925
1925.Ising.ZP.31
- Ising,
Beitrag zur Theorie des Ferromagnetismus, Zeit. für Physik 31, 253 (1925), doi:10.1007/BF02980577.
| Extended data | |
|---|---|
| Author | E. Ising |
| Title | Beitrag zur Theorie des Ferromagnetismus |
| Journal | Zeitschrift für Physik |
| Volume | 31 |
| Pages | 253-258 |
| Year | 1925 |
| doi | 10.1007/BF02980577 |
| Publication date | 1925 |
| Submission date | 1925-12-09 |
@article{1925.Ising.ZP.31,
author = {Ising, E.},
affiliation = {Hamburg},
title = {{Beitrag zur Theorie des Ferromagnetismus}},
journal = {Zeitschrift f\"ur Physik},
publisher = {Springer Berlin / Heidelberg},
issn = {0939-7922},
pages = {253-258},
volume = {31},
issue = {1},
url = {http://dx.doi.org/10.1007/BF02980577},
year = {1925}
}1928
1928.Heisenberg.ZP.49
- Heisenberg,
Zur Theorie des Ferromagnetismus,
- Phys. 49, 619 (1928), doi:10.1007/BF01328601.
| Extended data | |
|---|---|
| Author | W. Heisenberg |
| Title | Zur Theorie des Ferromagnetismus |
| Journal | Z. Phys. |
| Volume | 49 |
| Pages | 619 |
| Year | 1928 |
| doi | 10.1007/BF01328601 |
| Publication date | |
| Submission date |
@article{1928.Heisenberg.ZP.49,
author = {W. Heisenberg},
title = {{Zur Theorie des Ferromagnetismus}},
journal = {Z. Phys.},
year = {1928},
volume = {49},
pages = {619},
doi = {10.1007/BF01328601}
}1930
1930.Bloch.ZP.61
- Bloch,
Zur Theorie des Ferromagnetismus, Zeit. für Physik 61, 206 (1930), doi:10.1007/BF01339661.
| Extended data | |
|---|---|
| Author | Felix Bloch |
| Title | Zur Theorie des Ferromagnetismus |
| Journal | Zeitschrift für Physik |
| Volume | 61 |
| Pages | 206-219 |
| Year | 1930 |
| doi | 10.1007/BF01339661 |
| Publication date | 1930-03 |
| Submission date | 1930-02-01 |
@Article{1930.Bloch.ZP.61,
author = {F. Bloch},
title = {{Zur Theorie des Ferromagnetismus}},
journal = {Z. Phys.},
year = {1930},
volume = {61},
pages = {206}
}Missing out on eternal fame: Bloch makes the fateful (over)simplification after equation (8b) on p. 211: to quote, Dies suchen wir näherungsweise zu lösen, indem wir… die N Gleichungen (8b) weglassen, i.e. These we try to solve approximately, … by neglecting the N conditions (8b).
1931
1931.Bethe.ZP.71
-
- Bethe,
Zur Theorie der Metalle. I. Eigenwerte und Eigenfunktionen der linearen Atomkette, Zeit. für Physik 71, 205 (1931), doi:10.1007/BF01341708.
| Extended data | |
|---|---|
| Author | Hans Albrecht Bethe |
| Title | Zur Theorie der Metalle. I. Eigenwerte und Eigenfunktionen der linearen Atomkette |
| Journal | Zeit. für Physik |
| Volume | 71 |
| Pages | 205-226 |
| Year | 1931 |
| doi | 10.1007/BF01341708 |
| Publication date | 1931-03 |
| Submission date | 1931-06-17 |
Translations into English:
- by Teunis C. Dorlas (2009): On the Theory of Metals. I. Eigenvalues and eigenfunctions of a linear chain of atoms
@Article{1931.Bethe.ZP.71,
author = {H. A. Bethe},
title = {Zur {T}heorie der {M}etalle. I. {E}igenwerte und {E}igenfunktionen der linearen {A}tomkette},
journal = {Zeit. f\"ur Physik},
year = {1931},
volume = {71},
pages = {205},
doi = {10.1007/BF01341708}
}Impossible chronology: the article appeared in issue 3-4 of volume 71 of the journal, which carries the date March 1931. However, Bethe signs off dated 13 June 1931 at the end of the article, and the article header mentions 17 June 1931 as reception (in modern parlance: submission) date.
1938
1938.Hulthen.AMAF.26A
- Hulth{\'e}n,
\"U}ber das Austauschproblem eines Kristalles, Arkiv Mat. Astron. Fysik 26A, 1 (1938), doi:https://doi.org/.
| Extended data | |
|---|---|
| Author | L. Hulth{\'e}n |
| Title | \"U}ber das Austauschproblem eines Kristalles |
| Journal | Arkiv Mat. Astron. Fysik |
| Volume | 26A |
| Pages | 1 |
| Year | 1938 |
| doi | https://doi.org/ |
| Publication date | |
| Submission date |
@Article{1938.Hulthen.AMAF.26A,
author = {L. Hulth{\'e}n},
title = {{{\"U}ber das Austauschproblem eines Kristalles}},
journal = {Arkiv Mat. Astron. Fysik},
year = {1938},
volume = {26A},
pages = {1},
doi = "",
}1938.Sauter.AP.425
- Sauter,
Zur Theorie der idealen Magnetisierungskurve, Ann. Phys. 425, 672 (1938), doi:10.1002/andp.19384250713.
| Extended data | |
|---|---|
| Author | Fritz Sauter |
| Title | Zur Theorie der idealen Magnetisierungskurve |
| Journal | Annalen der Physik |
| Volume | 425 |
| Pages | 672-681 |
| Year | 1938 |
| doi | 10.1002/andp.19384250713 |
| Publication date | |
| Submission date | 1938-08-31 |
@Article{1938.Sauter.AP.425,
author = {Sauter, Fritz},
title = {Zur Theorie der idealen Magnetisierungskurve},
journal = {Annalen der Physik},
volume = {425},
number = {7},
year = {1938},
pages = {672-681},
doi = {10.1002/andp.19384250713}
}Complexity too much for Sauter: his complaints about Bethe's approach begin at the bottom of the first page of the article.
1952
1952.Anderson.PR.86
Anderson, P. W., An Approximate Quantum Theory of the Antiferromagnetic Ground State, Phys. Rev. 86, 694–701 (1952), doi:10.1103/PhysRev.86.694.
| Extended data | |
|---|---|
| Author | Anderson, P. W. |
| Title | An Approximate Quantum Theory of the Antiferromagnetic Ground State |
| Journal | Phys. Rev. |
| Volume | 86 |
| Pages | 694–701 |
| Year | 1952 |
| doi | 10.1103/PhysRev.86.694 |
| Publication date | |
| Submission date |
@Article{1952.Anderson.PR.86,
title = {An Approximate Quantum Theory of the Antiferromagnetic Ground State},
author = {Anderson, P. W.},
journal = {Phys. Rev.},
volume = {86},
number = {5},
pages = {694--701},
numpages = {7},
year = {1952},
OPTmonth = {Jun},
doi = {10.1103/PhysRev.86.694},
publisher = {American Physical Society}
}1958
1958.Orbach.PR.112
Orbach, R. , Linear Antiferromagnetic Chain with Anisotropic Coupling, Phys. Rev. 112, 309–316 (1958), doi:10.1103/PhysRev.112.309.
| Extended data | |
|---|---|
| Author | Orbach, R. |
| Title | Linear Antiferromagnetic Chain with Anisotropic Coupling |
| Journal | Phys. Rev. |
| Volume | 112 |
| Pages | 309–316 |
| Year | 1958 |
| doi | 10.1103/PhysRev.112.309 |
| Publication date | |
| Submission date |
@Article{1958.Orbach.PR.112,
title = {Linear Antiferromagnetic Chain with Anisotropic Coupling},
author = {Orbach, R. },
journal = {Phys. Rev.},
volume = {112},
number = {2},
pages = {309--316},
numpages = {7},
year = {1958},
OPTmonth = {Oct},
doi = {10.1103/PhysRev.112.309},
publisher = {American Physical Society}
}1962
1962.desCloizeaux.PR.128
des Cloizeaux, J. and Pearson, J. J., Spin-Wave Spectrum of the Antiferromagnetic Linear Chain, Phys. Rev. 128, 2131–2135 (1962), doi:10.1103/PhysRev.128.2131.
| Extended data | |
|---|---|
| Author | des Cloizeaux, J. and Pearson, J. J. |
| Title | Spin-Wave Spectrum of the Antiferromagnetic Linear Chain |
| Journal | Phys. Rev. |
| Volume | 128 |
| Pages | 2131–2135 |
| Year | 1962 |
| doi | 10.1103/PhysRev.128.2131 |
| Publication date | |
| Submission date |
@Article{1962.desCloizeaux.PR.128,
title = {Spin-Wave Spectrum of the Antiferromagnetic Linear Chain},
author = {des Cloizeaux, J. and Pearson, J. J.},
journal = {Phys. Rev.},
volume = {128},
number = {5},
pages = {2131--2135},
numpages = {4},
year = {1962},
OPTmonth = {Dec},
doi = {10.1103/PhysRev.128.2131},
publisher = {American Physical Society}
}1963
1963.Lieb.PR.130.1
Lieb, E. H. and Liniger, W., Exact Analysis of an Interacting Bose Gas. I. The General Solution and the Ground State, Phys. Rev. 130, 1605–1616 (1963), doi:10.1103/PhysRev.130.1605.
| Extended data | |
|---|---|
| Author | Lieb, E. H. and Liniger, W. |
| Title | Exact Analysis of an Interacting Bose Gas. I. The General Solution and the Ground State |
| Journal | Phys. Rev. |
| Volume | 130 |
| Pages | 1605–1616 |
| Year | 1963 |
| doi | 10.1103/PhysRev.130.1605 |
| Publication date | |
| Submission date |
@Article{1963.Lieb.PR.130.1,
title = {{Exact Analysis of an Interacting Bose Gas. I. The General Solution and the Ground State}},
author = {Lieb, E. H. and Liniger, W.},
journal = {Phys. Rev.},
volume = {130},
number = {4},
pages = {1605--1616},
numpages = {11},
year = {1963},
OPTmonth = {May},
doi = {10.1103/PhysRev.130.1605},
publisher = {American Physical Society}
}1963.Lieb.PR.130.2
Lieb, E. H., Exact Analysis of an Interacting Bose Gas. II. The Excitation Spectrum, Phys. Rev. 130, 1616–1624 (1963), doi:10.1103/PhysRev.130.1616.
| Extended data | |
|---|---|
| Author | Lieb, E. H. |
| Title | Exact Analysis of an Interacting Bose Gas. II. The Excitation Spectrum |
| Journal | Phys. Rev. |
| Volume | 130 |
| Pages | 1616–1624 |
| Year | 1963 |
| doi | 10.1103/PhysRev.130.1616 |
| Publication date | |
| Submission date |
@Article{1963.Lieb.PR.130.2,
title = {{Exact Analysis of an Interacting Bose Gas. II. The Excitation Spectrum}},
author = {Lieb, E. H.},
journal = {Phys. Rev.},
volume = {130},
number = {4},
pages = {1616--1624},
numpages = {8},
year = {1963},
OPTmonth = {May},
doi = {10.1103/PhysRev.130.1616},
publisher = {American Physical Society}
}1964
1964.Griffiths.PR.133
Griffiths, R. B., Magnetization Curve at Zero Temperature for the Antiferromagnetic Heisenberg Linear Chain, Phys. Rev. 133, A768–A775 (1964), doi:10.1103/PhysRev.133.A768.
| Extended data | |
|---|---|
| Author | Griffiths, R. B. |
| Title | Magnetization Curve at Zero Temperature for the Antiferromagnetic Heisenberg Linear Chain |
| Journal | Phys. Rev. |
| Volume | 133 |
| Pages | A768–A775 |
| Year | 1964 |
| doi | 10.1103/PhysRev.133.A768 |
| Publication date | |
| Submission date |
@Article{1964.Griffiths.PR.133,
title = {Magnetization Curve at Zero Temperature for the Antiferromagnetic Heisenberg Linear Chain},
author = {Griffiths, R. B.},
journal = {Phys. Rev.},
volume = {133},
number = {3A},
pages = {A768--A775},
numpages = {7},
year = {1964},
OPTmonth = {Feb},
doi = {10.1103/PhysRev.133.A768},
publisher = {American Physical Society}
}1964.McGuire.JMP.5
-
- McGuire,
Study of Exactly Soluble One-Dimensional N-Body Problems,
- Math. Phys. 5, 622-636 (1964), doi:10.1063/1.1704156.
| Extended data | |
|---|---|
| Author | J. B. McGuire |
| Title | Study of Exactly Soluble One-Dimensional N-Body Problems |
| Journal | J. Math. Phys. |
| Volume | 5 |
| Pages | 622-636 |
| Year | 1964 |
| doi | 10.1063/1.1704156 |
| Publication date | |
| Submission date |
@article{1964.McGuire.JMP.5,
author = {J. B. McGuire},
collaboration = {},
title = {{Study of Exactly Soluble One-Dimensional N-Body Problems}},
publisher = {AIP},
year = {1964},
journal = {J. Math. Phys.},
volume = {5},
number = {5},
pages = {622-636},
OPTurl = {http://link.aip.org/link/?JMP/5/622/1},
doi = {10.1063/1.1704156}
}1966
1966.desCloizeaux.JMP.7.1
- Des Cloizeaux and M. Gaudin,
Anisotropic Linear Magnetic Chain,
- Math. Phys. 7, 1384-1400 (1966), doi:10.1063/1.1705048.
| Extended data | |
|---|---|
| Author | J. Des Cloizeaux and M. Gaudin |
| Title | Anisotropic Linear Magnetic Chain |
| Journal | J. Math. Phys. |
| Volume | 7 |
| Pages | 1384-1400 |
| Year | 1966 |
| doi | 10.1063/1.1705048 |
| Publication date | |
| Submission date |
@article{1966.desCloizeaux.JMP.7.1,
author = {J. Des Cloizeaux and M. Gaudin},
collaboration = {},
title = {{Anisotropic Linear Magnetic Chain}},
publisher = {AIP},
year = {1966},
journal = {J. Math. Phys.},
volume = {7},
number = {8},
pages = {1384-1400},
OPTurl = {http://link.aip.org/link/?JMP/7/1384/1},
doi = {10.1063/1.1705048}
}1966.Yang.PR.150.1
Yang, C. N. and Yang, C. P., One-Dimensional Chain of Anisotropic Spin-Spin Interactions. I. Proof of Bethe's Hypothesis for Ground State in a Finite System, Phys. Rev. 150, 321–327 (1966), doi:10.1103/PhysRev.150.321.
| Extended data | |
|---|---|
| Author | Yang, C. N. and Yang, C. P. |
| Title | One-Dimensional Chain of Anisotropic Spin-Spin Interactions. I. Proof of Bethe's Hypothesis for Ground State in a Finite System |
| Journal | Phys. Rev. |
| Volume | 150 |
| Pages | 321–327 |
| Year | 1966 |
| doi | 10.1103/PhysRev.150.321 |
| Publication date | |
| Submission date |
@Article{1966.Yang.PR.150.1,
title = {{One-Dimensional Chain of Anisotropic Spin-Spin Interactions. I. Proof of Bethe's Hypothesis for Ground State in a Finite System}},
author = {Yang, C. N. and Yang, C. P.},
journal = {Phys. Rev.},
volume = {150},
number = {1},
pages = {321--327},
numpages = {6},
year = {1966},
OPTmonth = {Oct},
doi = {10.1103/PhysRev.150.321},
publisher = {American Physical Society}
}1966.Yang.PR.150.2
Yang, C. N. and Yang, C. P., One-Dimensional Chain of Anisotropic Spin-Spin Interactions. II. Properties of the Ground-State Energy Per Lattice Site for an Infinite System, Phys. Rev. 150, 327–339 (1966), doi:10.1103/PhysRev.150.327.
| Extended data | |
|---|---|
| Author | Yang, C. N. and Yang, C. P. |
| Title | One-Dimensional Chain of Anisotropic Spin-Spin Interactions. II. Properties of the Ground-State Energy Per Lattice Site for an Infinite System |
| Journal | Phys. Rev. |
| Volume | 150 |
| Pages | 327–339 |
| Year | 1966 |
| doi | 10.1103/PhysRev.150.327 |
| Publication date | |
| Submission date |
@Article{1966.Yang.PR.150.2,
title = {{One-Dimensional Chain of Anisotropic Spin-Spin Interactions. II. Properties of the Ground-State Energy Per Lattice Site for an Infinite System}},
author = {Yang, C. N. and Yang, C. P.},
journal = {Phys. Rev.},
volume = {150},
number = {1},
pages = {327--339},
numpages = {12},
year = {1966},
OPTmonth = {Oct},
doi = {10.1103/PhysRev.150.327},
publisher = {American Physical Society}
}1966.Yang.PR.151
Yang, C. N. and Yang, C. P., One-Dimensional Chain of Anisotropic Spin-Spin Interactions. III. Applications, Phys. Rev. 151, 258–264 (1966), doi:10.1103/PhysRev.151.258.
| Extended data | |
|---|---|
| Author | Yang, C. N. and Yang, C. P. |
| Title | One-Dimensional Chain of Anisotropic Spin-Spin Interactions. III. Applications |
| Journal | Phys. Rev. |
| Volume | 151 |
| Pages | 258–264 |
| Year | 1966 |
| doi | 10.1103/PhysRev.151.258 |
| Publication date | |
| Submission date |
@Article{1966.Yang.PR.151,
title = {One-Dimensional Chain of Anisotropic Spin-Spin Interactions. III. Applications},
author = {Yang, C. N. and Yang, C. P.},
journal = {Phys. Rev.},
volume = {151},
number = {1},
pages = {258--264},
numpages = {6},
year = {1966},
OPTmonth = {Nov},
doi = {10.1103/PhysRev.151.258},
publisher = {American Physical Society}
}1967
1967.Gaudin.PLA.24
- Gaudin,
Un systeme à une dimension de fermions en interaction, Phys. Lett. A 24, 55 (1967), doi:10.1016/0375-9601(67)90193-4.
| Extended data | |
|---|---|
| Author | M. Gaudin |
| Title | Un systeme à une dimension de fermions en interaction |
| Journal | Phys. Lett. A |
| Volume | 24 |
| Pages | 55-56 |
| Year | 1967 |
| doi | 10.1016/0375-9601(67)90193-4 |
| Publication date | 1967-01-02 |
| Submission date | 1966-11-24 |
@Article{1967.Gaudin.PLA.24,
title = "Un systeme à une dimension de fermions en interaction",
journal = "Phys. Lett. A",
volume = "24",
number = "1",
pages = "55 - 56",
year = "1967",
note = "",
OPTissn = "0375-9601",
doi = "10.1016/0375-9601(67)90193-4",
OPTurl = "http://www.sciencedirect.com/science/article/pii/0375960167901934",
author = "M. Gaudin"
}1967.Yang.PRL.19
Yang, C. N., Some Exact Results for the Many-Body Problem in one Dimension with Repulsive Delta-Function Interaction, Phys. Rev. Lett. 19, 1312–1315 (1967), doi:10.1103/PhysRevLett.19.1312.
| Extended data | |
|---|---|
| Author | Yang, C. N. |
| Title | Some Exact Results for the Many-Body Problem in one Dimension with Repulsive Delta-Function Interaction |
| Journal | Phys. Rev. Lett. |
| Volume | 19 |
| Pages | 1312–1315 |
| Year | 1967 |
| doi | 10.1103/PhysRevLett.19.1312 |
| Publication date | |
| Submission date |
@Article{1967.Yang.PRL.19,
title = {{Some Exact Results for the Many-Body Problem in one Dimension with Repulsive Delta-Function Interaction}},
author = {Yang, C. N.},
journal = {Phys. Rev. Lett.},
volume = {19},
number = {23},
pages = {1312--1315},
numpages = {3},
year = {1967},
OPTmonth = {Dec},
doi = {10.1103/PhysRevLett.19.1312},
publisher = {American Physical Society}
}1968
1968.Lieb.PRL.20
Lieb, E. H. and Wu, F. Y., Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension, Phys. Rev. Lett. 20, 1445–1448 (1968), doi:10.1103/PhysRevLett.20.1445.
| Extended data | |
|---|---|
| Author | Lieb, E. H. and Wu, F. Y. |
| Title | Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension |
| Journal | Phys. Rev. Lett. |
| Volume | 20 |
| Pages | 1445–1448 |
| Year | 1968 |
| doi | 10.1103/PhysRevLett.20.1445 |
| Publication date | |
| Submission date |
@Article{1968.Lieb.PRL.20,
title = {{Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension}},
author = {Lieb, E. H. and Wu, F. Y.},
journal = {Phys. Rev. Lett.},
volume = {20},
number = {25},
pages = {1445--1448},
numpages = {3},
year = {1968},
OPTmonth = {Jun},
doi = {10.1103/PhysRevLett.20.1445},
publisher = {American Physical Society}
}1969
1969.Yang.JMP.10
-
- Yang and C. P. Yang,
Thermodynamics of a One-Dimensional System of Bosons with Repulsive Delta-Function Interaction,
- Math. Phys. 10, 1115-1122 (1969), doi:10.1063/1.1664947.
| Extended data | |
|---|---|
| Author | C. N. Yang and C. P. Yang |
| Title | Thermodynamics of a One-Dimensional System of Bosons with Repulsive Delta-Function Interaction |
| Journal | J. Math. Phys. |
| Volume | 10 |
| Pages | 1115-1122 |
| Year | 1969 |
| doi | 10.1063/1.1664947 |
| Publication date | |
| Submission date |
@article{1969.Yang.JMP.10,
author = {C. N. Yang and C. P. Yang},
collaboration = {},
title = {{Thermodynamics of a One-Dimensional System of Bosons with Repulsive Delta-Function Interaction}},
publisher = {AIP},
year = {1969},
journal = {J. Math. Phys.},
volume = {10},
number = {7},
pages = {1115-1122},
OPTurl = {http://link.aip.org/link/?JMP/10/1115/1},
doi = {10.1063/1.1664947}
}1971
1971.Gaudin.JMP.12.I
- Gaudin,
Bose Gas in One Dimension. I. The Closure Property of the Scattering Wavefunctions,
- Math. Phys. 12, 1674-1676 (1971), doi:10.1063/1.1665790.
| Extended data | |
|---|---|
| Author | M. Gaudin |
| Title | Bose Gas in One Dimension. I. The Closure Property of the Scattering Wavefunctions |
| Journal | J. Math. Phys. |
| Volume | 12 |
| Pages | 1674-1676 |
| Year | 1971 |
| doi | 10.1063/1.1665790 |
| Publication date | |
| Submission date |
@article{1971.Gaudin.JMP.12.I,
author = {M. Gaudin},
collaboration = {},
title = {{Bose Gas in One Dimension. I. The Closure Property of the Scattering Wavefunctions}},
publisher = {AIP},
year = {1971},
journal = {J. Math. Phys.},
volume = {12},
number = {8},
pages = {1674-1676},
OPTurl = {http://link.aip.org/link/?JMP/12/1674/1},
doi = {10.1063/1.1665790}
}1971.Gaudin.JMP.12.II
- Gaudin,
Bose Gas in One Dimension. II. Orthogonality of the Scattering States,
- Math. Phys. 12, 1677-1680 (1971), doi:10.1063/1.1665791.
| Extended data | |
|---|---|
| Author | M. Gaudin |
| Title | Bose Gas in One Dimension. II. Orthogonality of the Scattering States |
| Journal | J. Math. Phys. |
| Volume | 12 |
| Pages | 1677-1680 |
| Year | 1971 |
| doi | 10.1063/1.1665791 |
| Publication date | |
| Submission date |
@article{1971.Gaudin.JMP.12.II,
author = {M. Gaudin},
collaboration = {},
title = {{Bose Gas in One Dimension. II. Orthogonality of the Scattering States}},
publisher = {AIP},
year = {1971},
journal = {J. Math. Phys.},
volume = {12},
number = {8},
pages = {1677-1680},
OPTurl = {http://link.aip.org/link/?JMP/12/1677/1},
doi = {10.1063/1.1665791}
}1971.Gaudin.PRL.26
Gaudin, M. , Thermodynamics of the Heisenberg-Ising Ring for $\Delta \ge 1$, Phys. Rev. Lett. 26, 1301–1304 (1971), doi:10.1103/PhysRevLett.26.1301.
| Extended data | |
|---|---|
| Author | Gaudin, M. |
| Title | Thermodynamics of the Heisenberg-Ising Ring for $\Delta \ge 1$ |
| Journal | Phys. Rev. Lett. |
| Volume | 26 |
| Pages | 1301–1304 |
| Year | 1971 |
| doi | 10.1103/PhysRevLett.26.1301 |
| Publication date | |
| Submission date |
@Article{1971.Gaudin.PRL.26,
title = {{Thermodynamics of the Heisenberg-Ising Ring for $\Delta \ge 1$}},
author = {Gaudin, M. },
journal = {Phys. Rev. Lett.},
volume = {26},
number = {21},
pages = {1301--1304},
numpages = {3},
year = {1971},
OPTmonth = {May},
doi = {10.1103/PhysRevLett.26.1301},
publisher = {American Physical Society}
}1971.Lai.PRL.26
Lai, C. K., Thermodynamics of Fermions in One Dimension with a $\delta{}$-Function Interaction, Phys. Rev. Lett. 26, 1472–1475 (1971), doi:10.1103/PhysRevLett.26.1472.
| Extended data | |
|---|---|
| Author | Lai, C. K. |
| Title | Thermodynamics of Fermions in One Dimension with a $\delta{}$-Function Interaction |
| Journal | Phys. Rev. Lett. |
| Volume | 26 |
| Pages | 1472–1475 |
| Year | 1971 |
| doi | 10.1103/PhysRevLett.26.1472 |
| Publication date | |
| Submission date |
@Article{1971.Lai.PRL.26,
title = {Thermodynamics of Fermions in One Dimension with a $\delta{}$-Function Interaction},
author = {Lai, C. K.},
journal = {Phys. Rev. Lett.},
volume = {26},
number = {24},
pages = {1472--1475},
numpages = {3},
year = {1971},
OPTmonth = {Jun},
doi = {10.1103/PhysRevLett.26.1472},
publisher = {American Physical Society}
}1971.Takahashi.PLA.36
- Takahashi,
Thermodynamics of the Heisenberg-Ising model for [Delta] < 1 in one dimension, Phys. Lett. A 36, 325 - 326 (1971), doi:10.1016/0375-9601(71)90531-7.
| Extended data | |
|---|---|
| Author | M. Takahashi |
| Title | Thermodynamics of the Heisenberg-Ising model for [Delta] < 1 in one dimension |
| Journal | Phys. Lett. A |
| Volume | 36 |
| Pages | 325 - 326 |
| Year | 1971 |
| doi | 10.1016/0375-9601(71)90531-7 |
| Publication date | |
| Submission date |
@article{1971.Takahashi.PLA.36,
title = "Thermodynamics of the Heisenberg-Ising model for [Delta] < 1 in one dimension",
journal = "Phys. Lett. A",
volume = "36",
number = "4",
pages = "325 - 326",
year = "1971",
note = "",
OPTissn = "0375-9601",
doi = "10.1016/0375-9601(71)90531-7",
OPTurl = "http://www.sciencedirect.com/science/article/B6TVM-46SPK7V-FG/2/7af0c012701ee9292b010485ce3bc434",
author = "M. Takahashi"
}1971.Takahashi.PTP.46
- Takahashi,
One-Dimensional Heisenberg Model at Finite Temperature, Prog. Theor. Phys. 46, 401-415 (1971), doi:10.1143/PTP.46.401.
| Extended data | |
|---|---|
| Author | M. Takahashi |
| Title | One-Dimensional Heisenberg Model at Finite Temperature |
| Journal | Prog. Theor. Phys. |
| Volume | 46 |
| Pages | 401-415 |
| Year | 1971 |
| doi | 10.1143/PTP.46.401 |
| Publication date | |
| Submission date |
@Article{1971.Takahashi.PTP.46,
title = {{One-Dimensional Heisenberg Model at Finite Temperature}},
author = {M. Takahashi},
journal = {Prog. Theor. Phys.},
volume = {46},
number = {2},
pages = {401-415},
numpages = {14},
year = {1971},
OPTurl = {http://ptp.ipap.jp/link?PTP/46/401/},
doi = {10.1143/PTP.46.401},
publisher = {Progress of Theoretical Physics}
}1972
1972.Baxter.AP.70.1
-
- Baxter,
Partition function of the Eight-Vertex lattice model, Ann. Phys. 70, 193 - 228 (1972), doi:10.1016/0003-4916(72)90335-1.
| Extended data | |
|---|---|
| Author | R. J. Baxter |
| Title | Partition function of the Eight-Vertex lattice model |
| Journal | Ann. Phys. |
| Volume | 70 |
| Pages | 193 - 228 |
| Year | 1972 |
| doi | 10.1016/0003-4916(72)90335-1 |
| Publication date | |
| Submission date |
@article{1972.Baxter.AP.70.1,
title = "Partition function of the Eight-Vertex lattice model",
journal = "Ann. Phys.",
volume = "70",
number = "1",
pages = "193 - 228",
year = "1972",
note = "",
OPTissn = "0003-4916",
doi = "10.1016/0003-4916(72)90335-1",
OPTurl = "http://www.sciencedirect.com/science/article/pii/0003491672903351",
author = "R. J. Baxter"
}1972.Baxter.AP.70.2
-
- Baxter,
One-dimensional anisotropic Heisenberg chain, Ann. Phys. 70, 323 - 337 (1972), doi:10.1016/0003-4916(72)90270-9.
| Extended data | |
|---|---|
| Author | R. J. Baxter |
| Title | One-dimensional anisotropic Heisenberg chain |
| Journal | Ann. Phys. |
| Volume | 70 |
| Pages | 323 - 337 |
| Year | 1972 |
| doi | 10.1016/0003-4916(72)90270-9 |
| Publication date | |
| Submission date |
@article{1972.Baxter.AP.70.2,
title = "One-dimensional anisotropic Heisenberg chain",
journal = "Ann. Phys.",
volume = "70",
number = "2",
pages = "323 - 337",
year = "1972",
note = "",
OPTissn = "0003-4916",
doi = "10.1016/0003-4916(72)90270-9",
OPTurl = "http://www.sciencedirect.com/science/article/B6WB1-4DF4Y97-SC/2/a6e18398300e5070640cc5dc1c6319b5",
author = "R. J. Baxter"
}1972.Johnson.PLA.38
J.D. Johnson and B.M. McCoy and C.K. Lai, On Takahashi's study of the thermodynamics of the Heisenberg-Ising ring for $\Delta < 1$, Phys. Lett. A 38, 143 - 144 (1972), doi:10.1016/0375-9601(72)90449-5.
| Extended data | |
|---|---|
| Author | J.D. Johnson and B.M. McCoy and C.K. Lai |
| Title | On Takahashi's study of the thermodynamics of the Heisenberg-Ising ring for $\Delta < 1$ |
| Journal | Phys. Lett. A |
| Volume | 38 |
| Pages | 143 - 144 |
| Year | 1972 |
| doi | 10.1016/0375-9601(72)90449-5 |
| Publication date | |
| Submission date |
@article{1972.Johnson.PLA.38,
title = {{On Takahashi's study of the thermodynamics of the Heisenberg-Ising ring for $\Delta < 1$}},
journal = "Phys. Lett. A",
volume = "38",
number = "3",
pages = "143 - 144",
year = "1972",
note = "",
OPTissn = "0375-9601",
doi = "10.1016/0375-9601(72)90449-5",
OPTurl = "http://www.sciencedirect.com/science/article/B6TVM-46SNJVN-F6/2/f5810b350b9699ad194a2c355ecd57a4",
author = "J.D. Johnson and B.M. McCoy and C.K. Lai"
}1972.Johnson.PRA.6
Johnson, J. D. and McCoy, B. M., Low-Temperature Thermodynamics of the $|\Delta|\ge 1$ {H}eisenberg-{I}sing Ring, Phys. Rev. A 6, 1613–1626 (1972), doi:10.1103/PhysRevA.6.1613.
| Extended data | |||
|---|---|---|---|
| Author | Johnson, J. D. and McCoy, B. M. | ||
| Title | Low-Temperature Thermodynamics of the $ | Δ | ≥ 1$ {H}eisenberg-{I}sing Ring |
| Journal | Phys. Rev. A | ||
| Volume | 6 | ||
| Pages | 1613–1626 | ||
| Year | 1972 | ||
| doi | 10.1103/PhysRevA.6.1613 | ||
| Publication date | |||
| Submission date |
@Article{1972.Johnson.PRA.6,
title = {Low-Temperature Thermodynamics of the $|\Delta|\ge 1$ {H}eisenberg-{I}sing Ring},
author = {Johnson, J. D. and McCoy, B. M.},
journal = {Phys. Rev. A},
volume = {6},
number = {4},
pages = {1613--1626},
numpages = {13},
year = {1972},
OPTmonth = {Oct},
doi = {10.1103/PhysRevA.6.1613},
publisher = {American Physical Society}
}1972.Takahashi.PLA.41
- Takahashi and M. Suzuki,
A reply to the comments of Johnson et al. on the thermodynamics of the Heisenberg-Ising ring for [Delta]<1, Phys. Lett. A 41, 81 - 82 (1972), doi:10.1016/0375-9601(72)90643-3.
| Extended data | |
|---|---|
| Author | M. Takahashi and M. Suzuki |
| Title | A reply to the comments of Johnson et al. on the thermodynamics of the Heisenberg-Ising ring for [Delta]<1 |
| Journal | Phys. Lett. A |
| Volume | 41 |
| Pages | 81 - 82 |
| Year | 1972 |
| doi | 10.1016/0375-9601(72)90643-3 |
| Publication date | |
| Submission date |
@article{1972.Takahashi.PLA.41,
title = "A reply to the comments of Johnson et al. on the thermodynamics of the Heisenberg-Ising ring for [Delta]<1",
journal = "Phys. Lett. A",
volume = "41",
number = "1",
pages = "81 - 82",
year = "1972",
note = "",
OPTissn = "0375-9601",
doi = "10.1016/0375-9601(72)90643-3",
OPTurl = "http://www.sciencedirect.com/science/article/B6TVM-46T9PWN-45/2/543cefd7dfee456d3941346a8b6e6e57",
author = "M. Takahashi and M. Suzuki"
}1972.Takahashi.PTP.48
- Takahashi and M. Suzuki,
One-Dimensional Anisotropic Heisenberg Model at Finite Temperatures, Prog. Theor. Phys. 48, 2187-2209 (1972), doi:10.1143/PTP.48.2187.
| Extended data | |
|---|---|
| Author | M. Takahashi and M. Suzuki |
| Title | One-Dimensional Anisotropic Heisenberg Model at Finite Temperatures |
| Journal | Prog. Theor. Phys. |
| Volume | 48 |
| Pages | 2187-2209 |
| Year | 1972 |
| doi | 10.1143/PTP.48.2187 |
| Publication date | |
| Submission date |
@Article{1972.Takahashi.PTP.48,
title = {{One-Dimensional Anisotropic Heisenberg Model at Finite Temperatures}},
author = {M. Takahashi and M. Suzuki},
journal = {Prog. Theor. Phys.},
volume = {48},
number = {6},
pages = {2187-2209},
numpages = {22},
year = {1972},
OPTurl = {http://ptp.ipap.jp/link?PTP/48/2187/},
doi = {10.1143/PTP.48.2187},
publisher = {Progress of Theoretical Physics}
}1981
1981.Faddeev.PLA.85
-
- Faddeev and L. A. Takhtajan,
What is the spin of a spin wave?, Phys. Lett. A 85, 375 (1981), doi:https://doi.org/.
| Extended data | |
|---|---|
| Author | L. D. Faddeev and L. A. Takhtajan |
| Title | What is the spin of a spin wave? |
| Journal | Phys. Lett. A |
| Volume | 85 |
| Pages | 375 |
| Year | 1981 |
| doi | https://doi.org/ |
| Publication date | |
| Submission date |
@Article{1981.Faddeev.PLA.85,
author = {L. D. Faddeev and L. A. Takhtajan},
title = {What is the spin of a spin wave?},
journal = {Phys. Lett. A},
year = {1981},
volume = {85},
pages = {375},
doi = {}
}1981.Gaudin.PRD.23
Gaudin, M. and McCoy, B. M. and Wu, T. T., Normalization sum for the Bethe's hypothesis wave functions of the Heisenberg-Ising chain, Phys. Rev. D 23, 417–419 (1981), doi:10.1103/PhysRevD.23.417.
| Extended data | |
|---|---|
| Author | Gaudin, M. and McCoy, B. M. and Wu, T. T. |
| Title | Normalization sum for the Bethe's hypothesis wave functions of the Heisenberg-Ising chain |
| Journal | Phys. Rev. D |
| Volume | 23 |
| Pages | 417–419 |
| Year | 1981 |
| doi | 10.1103/PhysRevD.23.417 |
| Publication date | |
| Submission date |
@Article{1981.Gaudin.PRD.23,
title = {{Normalization sum for the Bethe's hypothesis wave functions of the Heisenberg-Ising chain}},
author = {Gaudin, M. and McCoy, B. M. and Wu, T. T.},
journal = {Phys. Rev. D},
volume = {23},
number = {2},
pages = {417--419},
numpages = {2},
year = {1981},
OPTmonth = {Jan},
doi = {10.1103/PhysRevD.23.417},
publisher = {American Physical Society}
}1982
1982.Babujian.PLA.90
H.M. Babujian, Exact solution of the one-dimensional isotropic Heisenberg chain with arbitrary spins S, Phys. Lett. A 90, 479 (1982), doi:10.1016/0375-9601(82)90403-0.
| Extended data | |
|---|---|
| Author | H. M. Babujian |
| Title | Exact solution of the one-dimensional isotropic Heisenberg chain with arbitrary spins S |
| Journal | Phys. Lett. A |
| Volume | 90 |
| Pages | 479-482 |
| Year | 1982 |
| doi | 10.1016/0375-9601(82)90403-0 |
| Publication date | 1982-08-09 |
| Submission date | 1982-05-13 |
@article{1982.Babujian.PLA.90,
title = {{Exact solution of the one-dimensional isotropic Heisenberg chain with arbitrary spins S}},
journal = "Phys. Lett. A",
volume = "90",
number = "9",
pages = "479 - 482",
year = "1982",
note = "",
issn = "0375-9601",
doi = "http://dx.doi.org/10.1016/0375-9601(82)90403-0",
url = "http://www.sciencedirect.com/science/article/pii/0375960182904030",
author = "H.M. Babujian"
}1982.Korepin.CMP.86
Korepin, V. E., Calculation of norms of Bethe wave functions, Commun. Math. Phys. 86, 391-418 (1982), doi:10.1007/BF01212176.
| Extended data | |
|---|---|
| Author | Korepin, V. E. |
| Title | Calculation of norms of Bethe wave functions |
| Journal | Commun. Math. Phys. |
| Volume | 86 |
| Pages | 391-418 |
| Year | 1982 |
| doi | 10.1007/BF01212176 |
| Publication date | |
| Submission date |
@Article{1982.Korepin.CMP.86,
author = {Korepin, V. E.},
affiliation = {Service de Physique Th{\'e}orique, Division de la Physique C.E.N.-Saclay, Orme des Merisiers F-91191 Gif-sur-Yvette Cedex France},
title = {{Calculation of norms of Bethe wave functions}},
journal = {Commun. Math. Phys.},
publisher = {Springer Berlin / Heidelberg},
OPTissn = {0010-3616},
keyword = {Physics and Astronomy},
pages = {391-418},
volume = {86},
issue = {3},
doi = {10.1007/BF01212176},
OPTnote = {10.1007/BF01212176},
abstract = {A class of two dimensional completely integrable models of statistical mechanics and quantum field theory is considered. Eigenfunctions of the Hamiltonians are known for these models. Norms of these eigenfunctions in the finite box are calculated in the present paper. These models include in particular the quantum nonlinear Schr{\"o}dinger equation and the Heisenberg XXZ model.},
year = {1982}
}1988
1988.Sklyanin.JPA.21
-
- Sklyanin,
Boundary conditions for integrable quantum systems,
- Phys. A: Math. Gen. 21, 2375-2389 (1988), doi:10.1088/0305-4470/21/10/015.
| Extended data | |
|---|---|
| Author | E. K. Sklyanin |
| Title | Boundary conditions for integrable quantum systems |
| Journal | J. Phys. A: Math. Gen. |
| Volume | 21 |
| Pages | 2375-2389 |
| Year | 1988 |
| doi | 10.1088/0305-4470/21/10/015 |
| Publication date | |
| Submission date |
@article{1988.Sklyanin.JPA.21,
author = {E. K. Sklyanin},
title = {Boundary conditions for integrable quantum systems},
journal = {J. Phys. A: Math. Gen.},
volume = {21},
number = {10},
pages = {2375-2389},
OPTurl = {http://stacks.iop.org/0305-4470/21/2375},
year = {1988},
abstract = {A new class of boundary conditions is described for quantum systems integrable by means of the quantum inverse scattering (R-matrix) method. The method proposed allows the author to treat open quantum chains with appropriate boundary terms in the Hamiltonian. The general considerations are applied to the XXZ and XYZ models, the nonlinear Schrodinger equation and Toda chain.},
doi = {10.1088/0305-4470/21/10/015}
}1989
1989.Slavnov.TMP.79
-
- Slavnov,
Calculation of scalar products of wave functions and form factors in the framework of the algebraic {B}ethe {A}nsatz, Theor. Math. Phys. 79, 502 (1989), doi:10.1007/BF01016531.
| Extended data | |
|---|---|
| Author | N. A. Slavnov |
| Title | Calculation of scalar products of wave functions and form factors in the framework of the algebraic {B}ethe {A}nsatz |
| Journal | Theor. Math. Phys. |
| Volume | 79 |
| Pages | 502 |
| Year | 1989 |
| doi | 10.1007/BF01016531 |
| Publication date | |
| Submission date |
@Article{1989.Slavnov.TMP.79,
author = {N. A. Slavnov},
title = {Calculation of scalar products of wave functions and form factors in the framework of the algebraic {B}ethe {A}nsatz},
journal = {Theor. Math. Phys.},
year = {1989},
volume = {79},
pages = {502},
doi = {10.1007/BF01016531}
}1990
1990.Slavnov.TMP.82
-
- Slavnov,
Nonequal-time current correlation function in a one-dimensional Bose gas, Theor. Math. Phys. 82, 273 (1990), doi:10.1007/BF01029221.
| Extended data | |
|---|---|
| Author | N. A. Slavnov |
| Title | Nonequal-time current correlation function in a one-dimensional Bose gas |
| Journal | Theor. Math. Phys. |
| Volume | 82 |
| Pages | 273 |
| Year | 1990 |
| doi | 10.1007/BF01029221 |
| Publication date | |
| Submission date |
@Article{1990.Slavnov.TMP.82,
author = {N. A. Slavnov},
title = {Nonequal-time current correlation function in a one-dimensional Bose gas},
journal = {Theor. Math. Phys.},
year = {1990},
volume = {82},
pages = {273},
doi = {10.1007/BF01029221}
}1992
1992.Essler.JPA.25
-
-
- Essler and V. E. Korepin and K. Schoutens,
-
Fine structure of the Bethe ansatz for the spin-1/2 Heisenberg XXX model,
- Phys. A: Math. Gen. 25, 4115-4126 (1992), doi:10.1088/0305-4470/25/15/019.
| Extended data | |
|---|---|
| Author | F. H. L. Essler and V. E. Korepin and K. Schoutens |
| Title | Fine structure of the Bethe ansatz for the spin-1/2 Heisenberg XXX model |
| Journal | J. Phys. A: Math. Gen. |
| Volume | 25 |
| Pages | 4115-4126 |
| Year | 1992 |
| doi | 10.1088/0305-4470/25/15/019 |
| Publication date | |
| Submission date |
@article{1992.Essler.JPA.25,
author = {F. H. L. Essler and V. E. Korepin and K. Schoutens},
title = {{Fine structure of the Bethe ansatz for the spin-1/2 Heisenberg XXX model}},
journal = {J. Phys. A: Math. Gen.},
volume = {25},
number = {15},
pages = {4115-4126},
OPTurl = {http://stacks.iop.org/0305-4470/25/4115},
doi = {10.1088/0305-4470/25/15/019},
year = {1992},
abstract = {The authors analyse the Bethe ansatz equations for the two-particle sector of the spin 1/2 Heisenberg XXX model on a one-dimensional lattice of length N. They show that, beginning at a critical lattice length of N=21.86, new pairs of real solutions develop, whereas complex solutions start to disappear. The integers (that appear in the logarithmic form of the Bethe equations) of the new solutions do not fit into the conventional classification scheme. The total number of solutions in the two-particle sector remains unchanged and is in agreement with the claim that the SU(2) extended Bethe ansatz gives a complete set of 2N eigenstates.}
}1999
1999.Kitanine.NPB.554
- Kitanine and J. M. Maillet and V. Terras,
Form factors of the {XXZ} {H}eisenberg finite chain, Nucl. Phys. B 554, 647 - 678 (1999), doi:10.1016/S0550-3213(99)00295-3.
| Extended data | |
|---|---|
| Author | N. Kitanine and J. M. Maillet and V. Terras |
| Title | Form factors of the {XXZ} {H}eisenberg finite chain |
| Journal | Nucl. Phys. B |
| Volume | 554 |
| Pages | 647 - 678 |
| Year | 1999 |
| doi | 10.1016/S0550-3213(99)00295-3 |
| Publication date | |
| Submission date |
@article{1999.Kitanine.NPB.554,
title = "Form factors of the {XXZ} {H}eisenberg finite chain",
journal = "Nucl. Phys. B",
volume = "554",
number = "3",
pages = "647 - 678",
year = "1999",
note = "",
OPTissn = "0550-3213",
doi = "10.1016/S0550-3213(99)00295-3",
OPTurl = "http://www.sciencedirect.com/science/article/B6TVC-3XJM8N2-7/2/517b0d93846c030c0f2ee522749b9b46",
author = "N. Kitanine and J. M. Maillet and V. Terras",
keywords = "Integrable models",
keywords = "Correlation functions"
}2007
2007.Hagemans.JPA.40
- Hagemans and J.-S. Caux,
Deformed strings in the Heisenberg model,
- Phys. A: Math. Theor. 40, 14605 (2007), doi:10.1088/1751-8113/40/49/001.
| Extended data | |
|---|---|
| Author | R. Hagemans and J.-S. Caux |
| Title | Deformed strings in the Heisenberg model |
| Journal | J. Phys. A: Math. Theor. |
| Volume | 40 |
| Pages | 14605 |
| Year | 2007 |
| doi | 10.1088/1751-8113/40/49/001 |
| Publication date | 2007-11-20 |
| Submission date | 2007-07-20 |
@article{2007_Hagemans_JPA_40,
author={R. Hagemans and J.-S. Caux},
title={Deformed strings in the {H}eisenberg model},
journal={J. Phys. A: Math. Theor.},
volume={40},
number={49},
pages={14605},
OPTurl={http://stacks.iop.org/1751-8121/40/i=49/a=001},
doi={10.1088/1751-8113/40/49/001},
year={2007},
abstract={We investigate solutions to the Bethe equations for the isotropic S = 1/2 Heisenberg chain involving complex, string-like rapidity configurations of arbitrary length. Going beyond the traditional string hypothesis of undeformed strings, we describe a general procedure to construct eigenstates including strings with generic deformations, discuss general features of these solutions and provide a number of explicit examples including complete solutions for all wavefunctions of short chains. We finally investigate some singular cases and show from simple symmetry arguments that their contribution to zero-temperature correlation functions vanishes.}
}2008
2008.Caux.JSTAT.P08006
J.-S. Caux, J. Mossel and I. Pérez Castillo, The two-spinon transverse structure factor of the gapped Heisenberg antiferromagnetic chain,
- Stat. Mech.: Th. Exp. 2008, P08006, doi:10.1088/1742-5468/2008/08/P08006.
| Extended data | |
|---|---|
| Author | J.-S. Caux, J. Mossel and I. Pérez Castillo |
| Title | The two-spinon transverse structure factor of the gapped Heisenberg antiferromagnetic chain |
| Journal | J. Stat. Mech.: Th. Exp. |
| Volume | 2008 |
| Pages | P08006 |
| Year | 2008 |
| doi | 10.1088/1742-5468/2008/08/P08006 |
| Publication date | 2008-08-19 |
| Submission date | 2008-06-23 |
@article{2008_Caux_JSTAT_P08006,
author={J.-S. Caux and J. Mossel and I. P{\'e}rez Castillo},
title={{The two-spinon transverse structure factor of the gapped Heisenberg antiferromagnetic chain}},
journal={J. Stat. Mech.: Th. Exp.},
volume={2008},
number={08},
pages={P08006},
OPTurl={http://stacks.iop.org/1742-5468/2008/i=08/a=P08006},
doi={10.1088/1742-5468/2008/08/P08006},
year={2008},
abstract={We consider the transverse dynamical structure factor of the anisotropic Heisenberg spin-1/2 chain ( XXZ model) in the gapped antiferromagnetic regime (Δ>1). Specializing to the case of zero field, we use two independent approaches based on integrability (one valid for finite size, the other for the infinite lattice) to obtain the exact two-spinon part of this correlator. We discuss in particular its asymmetry with respect to the π/2-momentum line, its overall anisotropy dependence, and its contribution to sum rules.}
}2007.Pereira.JSTAT.P08022
-
- Pereira, J. Sirker, J.-S. Caux, R. Hagemans, J. M. Maillet, S. R. White and I. Affleck,
Dynamical structure factor at small q for the XXZ spin-1/2 chain,
- Stat. Mech.: Th. Exp. 2007, P08022, doi:10.1088/1742-5468/2007/08/P08022.
| Extended data | |
|---|---|
| Author | R. G. Pereira, J. Sirker, J.-S. Caux, R. Hagemans, J. M. Maillet, S. R. White and I. Affleck, |
| Title | Dynamical structure factor at small q for the XXZ spin-1/2 chain |
| Journal | J. Stat. Mech.: Th. Exp. |
| Volume | 2007 |
| Pages | P08022 |
| Year | 2007 |
| doi | 10.1088/1742-5468/2007/08/P08022 |
| Publication date | 2007-08-10 |
| Submission date | 2007-06-29 |
@article{2007_Pereira_JSTAT_P08022,
author={R. G. Pereira and J. Sirker and J.-S. Caux and R. Hagemans and J. M. Maillet and S. R. White and I. Affleck},
title={{Dynamical structure factor at small q for the XXZ spin-1/2 chain}},
journal={J. Stat. Mech.: Th. Exp.},
volume={2007},
number={08},
pages={P08022},
OPTurl={http://stacks.iop.org/1742-5468/2007/i=08/a=P08022},
year={2007},
}